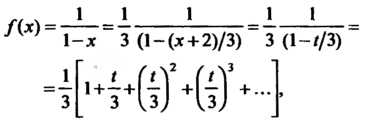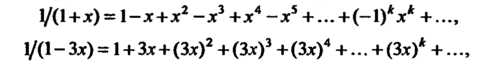24.4. Ряд Тейлора. Ряд Маклорена
Если функция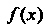 Разлагается в степенной ряд
Разлагается в степенной ряд
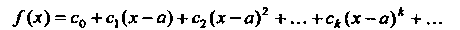
В некоторой окрестности точки а, т. е. в интервале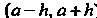 ), то коэффициенты
), то коэффициенты
Этого ряда определяются по формулам
(24.19)
Следовательно,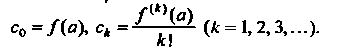
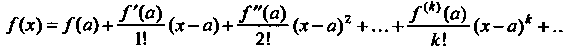 (24.20)
(24.20)
Ряд, стоящий в правой части формулы (24.20), называется рядом Тейлора для функции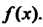
Равенство (24.20) выполняется (ряд Тейлора сходится к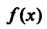 В интервале
В интервале 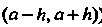 I, если остаток ряда Тейлора
I, если остаток ряда Тейлора
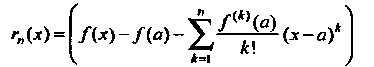
Стремится к нулю при неограниченном возрастании и:
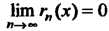
При всех х из интервала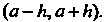
Достаточное условие разложимости функции в ряд Тейлора. Если функция f(x) бесконечно дифференцируема в интервале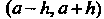 И ее производные
И ее производные
Равномерно ограничены в этом интервале, т. е. существует такое положительное число С (не зависящее от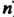 ), что
), что
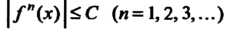
При всех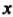 Из
Из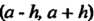 , то верно равенство (24.20) во всем интервале
, то верно равенство (24.20) во всем интервале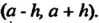
Формула (24.20) в частном случае при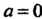 Определяет разложение функции в ряд Маклорена:
Определяет разложение функции в ряд Маклорена:
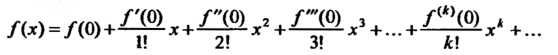 (24.21)
(24.21)
.При разложении функций в степенные ряды часто используется формула
(24.10) и разложения в ряд Маклорена следующих функций:
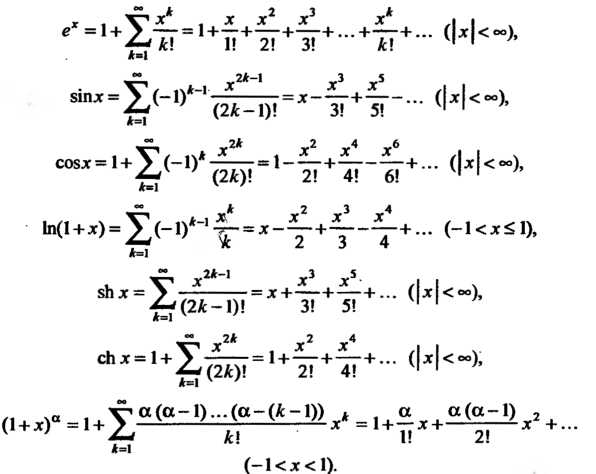
Пример 24.15. Разложить в ряд по степеням х функцию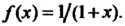 Воспользуемся разложением (24.10). В формуле
Воспользуемся разложением (24.10). В формуле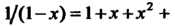
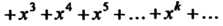 Запишем
Запишем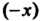 Вместо
Вместо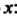
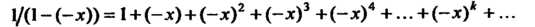
Таким образом, получено следующее разложение данной функции в степенной рад:
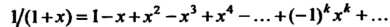 (24.22)
(24.22)
Этот ряд сходится при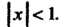
Замечание. Формулу (24.22) можно получить и другим путем. Рад 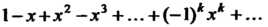 Является геометрическим рядом со знаменателем
Является геометрическим рядом со знаменателем
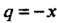 ; он сходится при
; он сходится при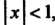 , его сумма
, его сумма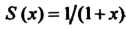 (получено по формуле
(получено по формуле
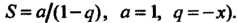
Пример 24.16. Разложить в ряд по степеням х функцию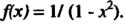 В формуле (24.22) вместо х запишем
В формуле (24.22) вместо х запишем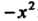
Полученный ряд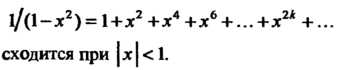
Замечание. Этот пример можно решить и другим способом. Так как
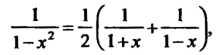
То в соответствии с разложениями (24.10) и (24.22) по определению суммы степенных рядов (формула (24.13)) получаем
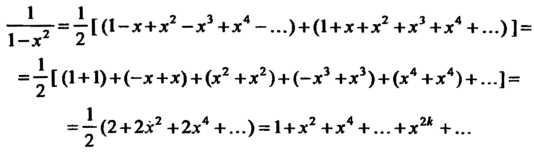
Пример 24.17. Разложить в ряд по степеням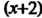 Функцию
Функцию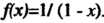 Преобразуем данную функцию следующим образом:
Преобразуем данную функцию следующим образом: 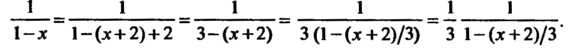
Введем новую переменную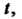 Полагая
Полагая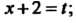 Воспользуемся разложением
Воспользуемся разложением
(24.10), записывая в нем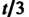 Вместо
Вместо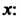
Или
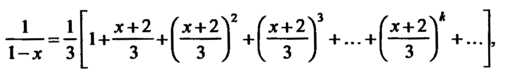
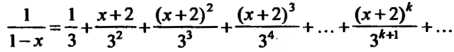
Ряд (1) сходится при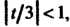 Т. е. при
Т. е. при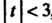 , или
, или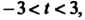 А ряд (2) сходит
А ряд (2) сходит
Ся при Или при
Или при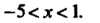
Пример 24.18. Разложить в ряд по степеням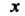 Функцию
Функцию 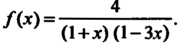 1 Разлагая данную функцию в сумму элементарных дробей, получаем
1 Разлагая данную функцию в сумму элементарных дробей, получаем 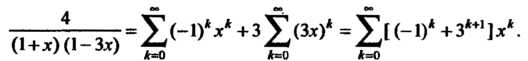
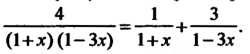 Так как
Так как
То по формуле (24.13) находим
Ряд (3) сходится при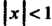 , ряд (4) сходится при
, ряд (4) сходится при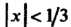 , поэтому ряд (5) также
, поэтому ряд (5) также
Сходится при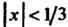 , т. е. в интервале
, т. е. в интервале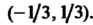
Пример 24.19. Найти разложение в степенной ряд функции 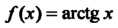 С помощью степенного ряда для
С помощью степенного ряда для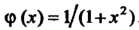 Прежде всего напишем степенной ряд для функции
Прежде всего напишем степенной ряд для функции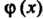 , записывая в формуле (24.10)
, записывая в формуле (24.10)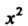 Вместо
Вместо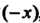 , получаем
, получаем
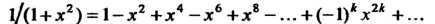
Этот ряд сходится при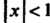 , т. е. в интервале
, т. е. в интервале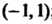 ; следовательно, его можно
; следовательно, его можно
Интегрировать почленно по любому промежутку, содержащемуся в указанном интервале. Интегрируя ряд по промежутку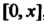 , где
, где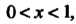 Находим
Находим
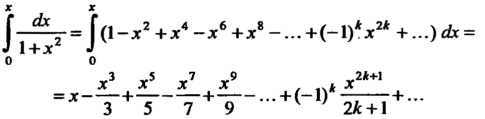
Поскольку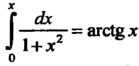 , то
, то
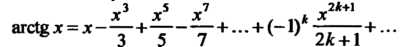
Этот ряд имеет радиус сходимости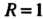 . На концах промежутка
. На концах промежутка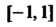 Ряд
Ряд
Также сходится. В частности, при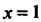 Получаем ряд
Получаем ряд 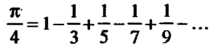
| < Предыдущая | Следующая > |
|---|