24.3. Степенные ряды. Действия над степенными рядами

Степенным называется функциональный ряд вида

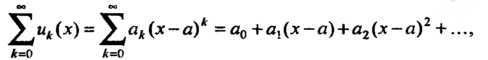(24.7)

Где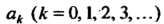- постоянные числа, называемые коэффициентами ряда.

При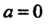Ряд принимает вид

Теорема 24.6 (признак Абеля). Если степенной ряд (24.8) сходится при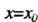 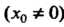|, то он сходится абсолютно и равномерно при любом х, для которого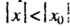

Радиусом сходимости ряда (24.8) называется число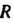Такое, что при 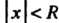ряд сходится, а при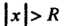Расходится. Интервал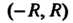В этом случае называ

Ется интервалом сходимости указанного ряда. На концах промежутка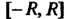Ряд

Может или сходится или расходится.

Если степенной ряд (24.8) сходится на всей числовой оси, то полагают,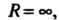 если он сходится только при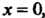Полагают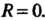Степенной ряд сходится абсо

Лютно и равномерно на любом отрезке, принадлежащем интервалу сходимости.

Аналогично определяется радиус и интервал сходимости для ряда (24.7): если при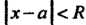Этот ряд сходится, а при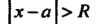Расходится, то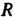- радиус

Его сходимости,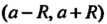- интервал сходимости.

Радиус сходимости степенного ряда находится с помощью признака Д’Аламбера или признака Коши.

Радиус сходимости можно вычислить по одной из формул:

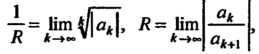(24.9)

Если соответствующий предел существует.

Простейшим примером степенного ряда является геометрический ряд Этот ряд сходится при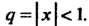Следовательно, для

Данного ряда радиус сходимости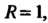А интервал сходимости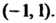Сумма этого

Ряда равна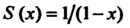(в соответствии с формулой

Поэтому для функции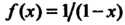Имеем следующее разложение в степенной ряд:

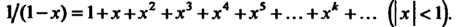(24.10)

Действия над степенными рядами. Рассмотрим степенные ряды

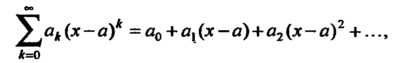(24.11)

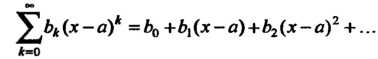(24.12)

С общим интервалом сходимости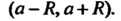

Сумма (разность) рядов (24.11) и (24.12) определяется соответственно формулами

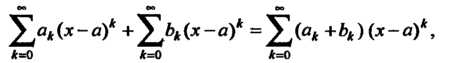(24.13)

(24.14)

А их произведение - формулой

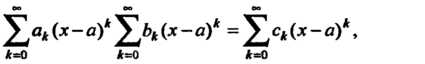(24.15)

Ряды (24.13) - (24.15) имеют тот же радиус сходимости, что и рады (24.11) и (24.12).

В частном случае, если ряды (24.11) и (24.12) совпадают, формула (24.15) обращается в формулу для возведения ряда в квадрат:

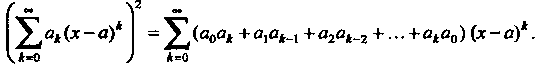
Степенной ряд в пределах промежутка сходимости можно возводить в степень с любым натуральным показателем т.

Степенной ряд (24.11) внутри его интервала сходимости можно почленно дифференцировать и интегрировать:

Ряды (24.17) и (24.18) имеют тот же радиус сходимости, что и ряд (24.11). Теорема 24.7. Если ряды (24.11) и (24.12) в окрестности точки х — а имеют одну и ту же сумму, то они тождественны, т. е.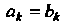

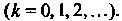
Эта теорема устанавливает единственность разложения функции в степенной ряд. Пример 24.9. Найти радиус сходимости степенного ряда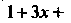

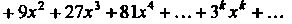
Это степенной рад вида (24.8), все коэффициенты его отличны от нуля. Воспользуемся первой из формул (24.9). Так как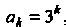,,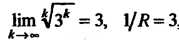 то

Радиус сходимости данного ряда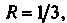А интервал сходимости (-1/3,1/3).

Замечание. Данный ряд является геометрическим радом со знаменателем 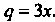Геометрический ряд сходится при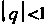, т. е. при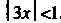, или при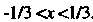

Пример 24.10. Найти радиус и интервал сходимости степенного рада

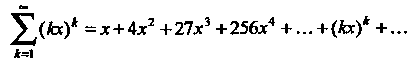
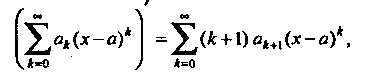
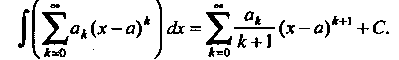
Применим вторую из формул (24.9). Поскольку

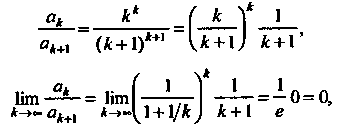
То радиус сходимости рада равен нулю. Ряд сходится в единственной точке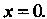

Замечание. Тот же результат можно получить и по первой формуле

Пример 24.11. Найти радиус и интервал сходимости степенного

Ряда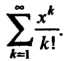

Так как>.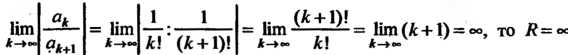

Ряд сходится при все>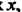. т. е. в интервале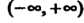

Пример 24.12. Найти область сходимости степенного ряда

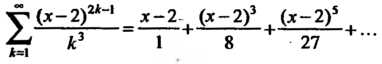
Применим признак Д’Аламбера, для чего найдем предел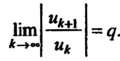 В данном случае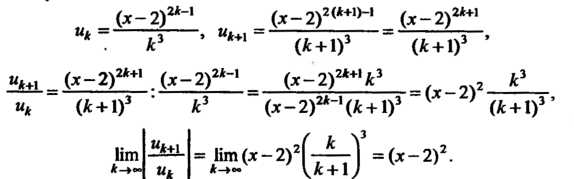

Так как пр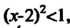иИли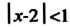, ряд сходится, а пр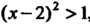и, или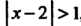

Ряд расходится, то в соответствии с определением радиус сходимости данного ряда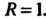Неравенство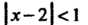Равносильно неравенствам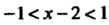Или

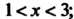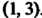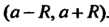Интервалом сходимости является интервал, Этот интервал можно найти, полагаяВ общем выраженииИсследуем сходи

Мость ряда на концах этого интервала. При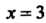Получаем ряд

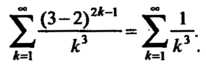
Этот ряд сходится (ряд Дирихле;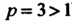). При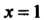Имеем

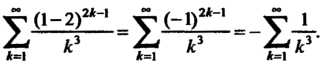
Этот ряд также сходится. Следовательно, данный ряд сходится при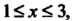Т. е.

Областью его сходимости является отрезок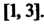

Пример 24.13. Найти область сходимости степенного ряда Применяем признак Д’Аламбера. В данном случае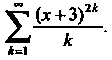

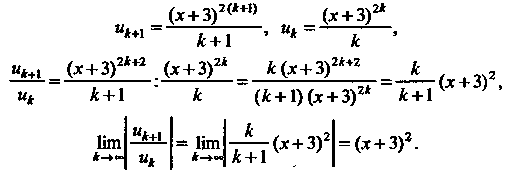
Поскольку при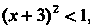, т. е. при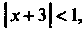Ряд сходится, а при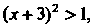

Т. е. при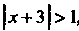, ряд расходится, то радиус сходимости данного ряд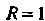а, а

Интервал сходимости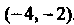. Исследуем сходимость ряда на концах промежут

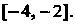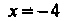КаПриПолучаем ряд

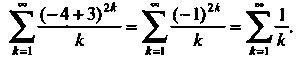
Этот ряд расходится (гармонический ряд). При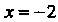Также получаем расходя

Щийся гармонический ряд. Следовательно, областью сходимости данного ряда является интервал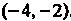

Пример 24.14. Найти область сходимости ряда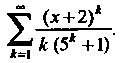 Применяем признак Д’Аламбера, считая х фиксированным. Поскольку

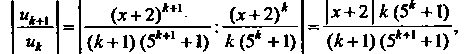
То

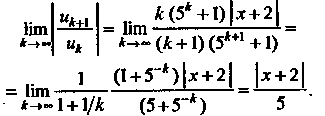
Ряд сходится, когда полученный предел меньше единицы, т. е.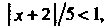Или

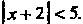Так как при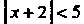Ряд сходится, а при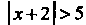Ряд расходится,

То радиус сходимости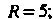Интервал ¦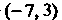Является интервалом сходимости.

Исследуем поведение ряда на концах промез^утка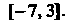При

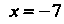
Получаем знакочередующийся ряд

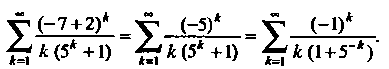
Этот рад удовлетворяет условиям признака Лейбница, поэтому он сходится. При 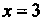Получаем ряд

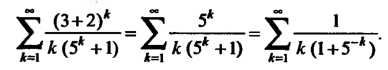
Полученный ряд расходится, так как каждый его член больше соответствующего члена расходящегося гармонического ряда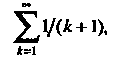Т. е.

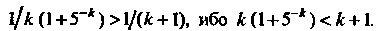
Следовательно, областью сходимости данного ряда является полуоткрытый промежуток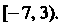

< Предыдущая		Следующая >