24.2. Равномерная сходимость функциональных рядов

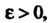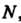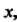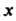Функциональный ряд (24.1) называется равномерно сходящимся в некотором промежутке, если, каково бы ни былоСуществует такое, не зависящее от Что приДля всехИз данного промежутка выполняется неравенство

Где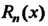- остаток ряда, определяемый формулой (24.3).

Теорема 24.1 (признак Вейерштрасса). Функциональный ряд (24.1) сходится абсолютно и равномерно в некотором промежутке, если существует сходящийся числовой ряд с положительными членами

(24.4)

Такой, что

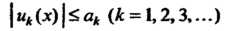(24.5)

Для всех х из данного промежутка

Ряд (24.4) в этом случае называется мажорантным рядом для ряда (24.1). Свойства функциональных рядов выражаются следующими теоремами. Теорема 24.2. Сумма равномерно сходящегося ряда функций, непрерывных в замкнутом промежутке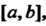Есть функция, непрерывная в данном промежутке.

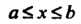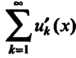Теорема 24.3. Если члены сходящегося ряда (24.1) имеют непрерывные производные приИ рядСходится равномерно в замкнутом промежутке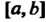, то ряд (24.1) в этом промежутке можно дифференцировать почленно:

(24.6)

Теорема 24.4. Если члены ряда (24.1) непрерывны при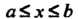И ряд этот

Сходится равномерно в замкнутом промежутке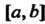, то его можно интегрировать почленно в данном промежутке:

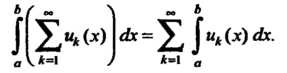
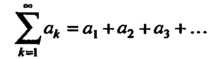
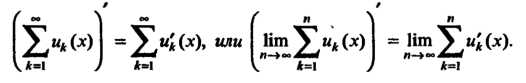
Теорема 24.5. Если ряд (24.1) сходится равномерно в некоторой области, и каждый член ряда имеет конечный предел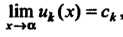, где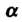- точка сгуще

Ния данной области, то к пределу можно перейти почленно, т. е.

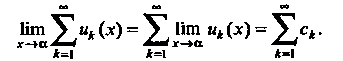
Пример 24.4. Исследовать, равномерно ли сходится ряд

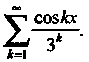
Так как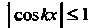Для всех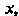То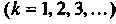, т. е. каждый

Член данного ряда не превышает соответствующего члена сходящегося числового ряда

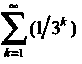(геометрический ряд,I. Последний ряд является мажорантным для

Данного ряда. В соответствии с признаком Вейернпрасса заключаем, что данный ряд сходится абсолютно и равномерно для всех*, т. е. на всей действительной оси.

Пример 24.5. Доказать, что сумма рядаявляется непре

Рывной функцией при всех х.

Прежде всего каждый член данного ряда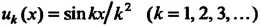Есть

Функция, непрерывная при всех х. Ряд сходится равномерно при всех х, поскольку

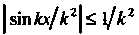И для данного ряда существует мажорантный ряд-

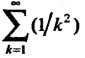Сходящийся числовой ряд с положительными членами (ряд Дирихле;).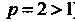

Согласно теореме 24.2, сумма данного ряда есть функция, непрерывная при всех х (как сумма равномерно сходящегося ряда непрерывных функций).

Пример 24.6. Можно ли почленно дифференцировать ряд

В области его сходимости?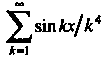

Каждый член данного ряда есть функция, дифференцируемая

При всех х, причем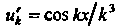

Составим ряд производных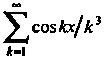Каждый член нового ряда -

Непрерывная функция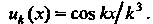Так как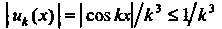

, то для него существует мажорантный ряд

Следовательно, ряд производных равномерно сходится при всех х, поэтому, согласно теореме 24.3, исходный ряд можно дифференцировать почленно. По формуле (24.6) получаем

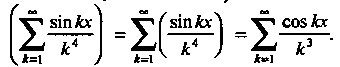
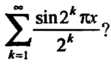
Этот ряд сходится равномерно при всех х, ибо для него существует мажорантный ряд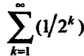(так как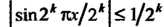). Каждый член ряда

Есть функция дифференцируемая, причем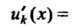

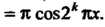Ряд производных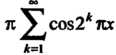Расходится в каждой точке, ибо ни в

Одной точке не выполняется необходимый признак сходимости (общий член к нулю не стремится). Следовательно, исходный ряд почленно дифференцировать нельзя.

Пример 24.8. Можно ли почленно интегрировать ряд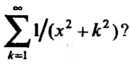

Каждый член данного ряда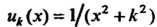Есть функция, непрерывная для

Всех х, ряд сходится равномерно на всей числовой оси. Действительно, так как для всех х выполняется неравенство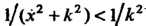, то для данного ряда сущест

Вует мажорантный ряд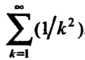

Таким образом, согласно теореме 24.4, данный ряд можно интегрировать по любому промежутку из его области сходимости, в частности по промежутку . Интегрируя, получаем

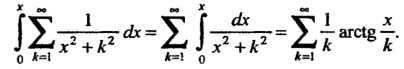
< Предыдущая		Следующая >