23.6. Некоторые числовые ряды и их суммы

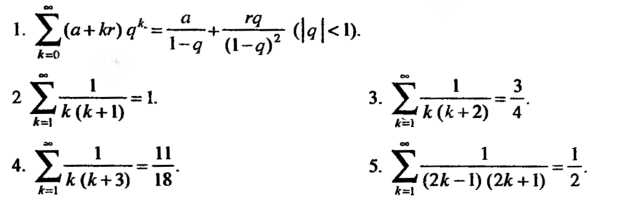
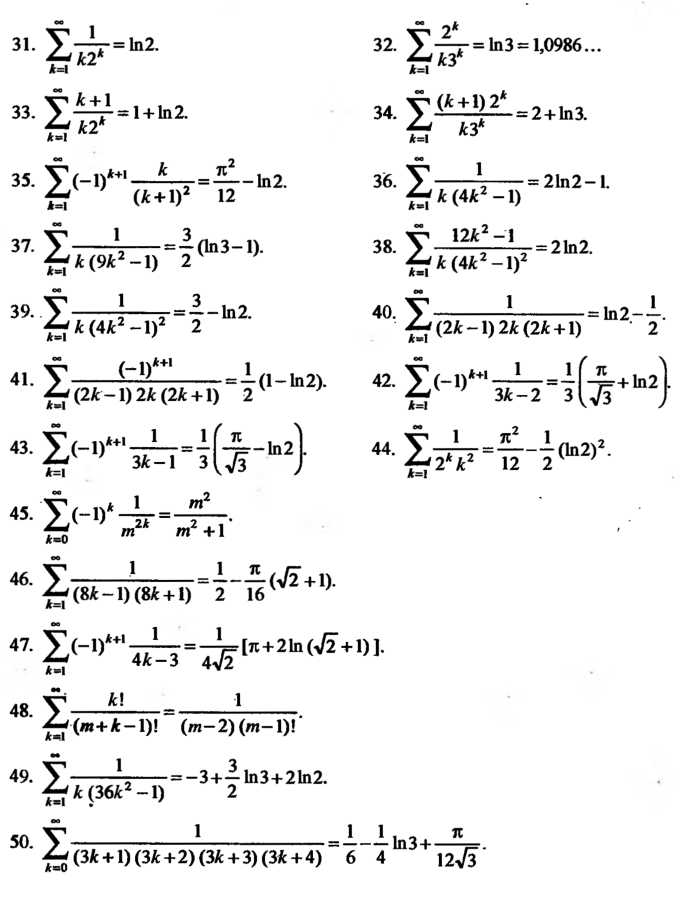
Гпава 24

ФУНКЦИОНАЛЬНЫЕ РЯДЫ

24.1. Сходимость функциональных рядов

Пусть дан функциональный ряд

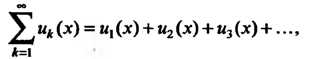(24.1)

Т. е. рад, члены которого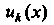— некоторые функции от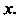

При каждом фиксированном значении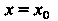Функциональный рад (24.1) ста

Новится числовым радом

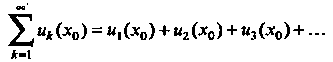(24.2)

Если рад (24.2) сходится, то значение аргумента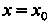Называется точкой схо

Димости ряда (24.1). Множество всех точек сходимости х функционального рада (24.1) называется его областью сходимости, а функция

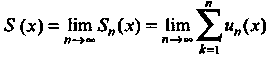
- суммой данного рада. Функция

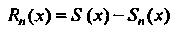(24.3)

Называется остатком рада (24.1).

Если ряд (24.2) расходится, то значение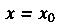Называется точкой расхо

Димости ряда (24.1).

В простейших случаях для определения области сходимости ряда (24.1) можно применять к нему известные признаки сходимости, считая х фиксированным. В частности, при применении признака Д’Аламбера или Коши случай, когда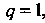 исследуется особо, с помощью других признаков сходимости.

Функциональныйрад (24.1) называется абсолютно сходящимся на множестве 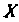, если при всех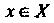Сходится рад из модулей его членов:

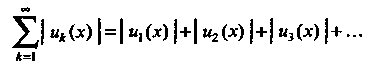
Пример 24.1. Найти область сходимости ряда

408

Данный ряд является геометрическим рядом со знаменателем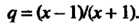Гео

Метрический ряд сходится тогда и только тогда, когда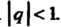Следовательно, данный рад

Сходится лишь в случае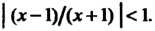Последнему неравенству равносильны нера

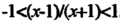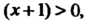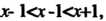Венства. ЕслиТо -Т. е.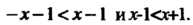

Второе из этих неравенств выполняется для всех х, первое верно только для *>0. Если

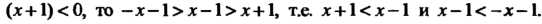Первое из полученных равенств противоречиво, второе выполняется при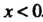. Но при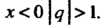

Таким образом, ряд сходится при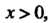Т. е. областью его сходимости является открытый промежуток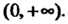(При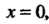Как и следовало ожидать, получаем

Расходящийся ряд).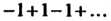

Пример 24.2. Найти область сходимости ряда

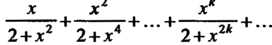
Общий член данного ряда определяется формулой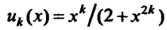. Так

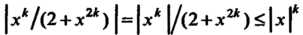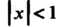КакПриИ ряд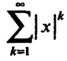Сходится при

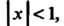То и данный ряд сходится дляПоскольку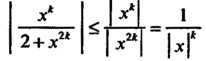

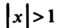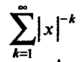ПриИ рядСходится при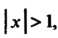То данный ряд сходится и для

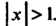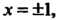ЕслиТо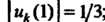; ряд расходится. Итак, данный ряд сходится

При всех л, кроме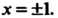

Пример 24.3. При каких* сходится ряд’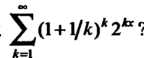

Применим к данному ряду признак Коши, для чего сначала найдем предел 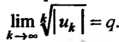Так как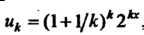,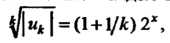То

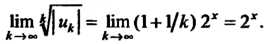
Найдем значения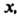При которых этот предел меньше 1, для чего решим неравенство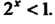Последнее неравенство выполняется для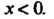При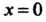Данный

Ряд принимает вид. Этот ряд расходится, так как для него не выпол

Нен необходимый признак сходимости (общий член к нулю не стремится:

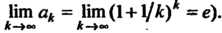Итак, ряд сходится при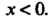

< Предыдущая		Следующая >