23.5. Действия над рядами

Суммой двух рядов

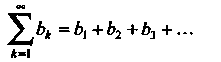(23.27)

Называется ряд

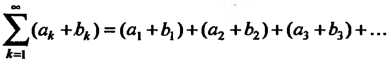(23.28)

Аналогично определяется разность двух рядов:

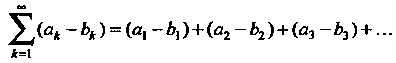(23.29)

Ряды (23.28) и (23.29) сходятся, если сходятся оба ряда (23.26), (23.27).

Если

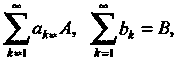
То

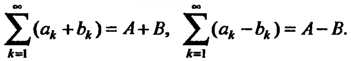
Произведением ряда (23.26) на число с называется ряд

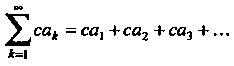(23.30)

Если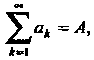То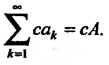

Произведением рядов (23.26) и (23.27) называется ряд

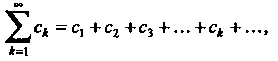(23.31)

Где

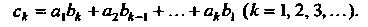(23.32)

Если ряды (23.26) и (23.27) сходятся абсолютно, то ряд (23.31) также сходится абсолютно и его сумма равна произведению сумм данных рядов.

Замечание. Если из двух сходящихся рядов (23.26) и (23.27) хоть один сходится абсолютно, то их произведение - сходящийся ряд.

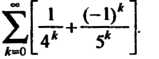
Этот ряд является суммой двух рядов:

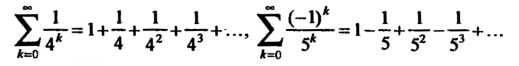
Каждый из этих рядов есть геометрический ряд

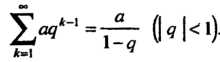
Цля первого ряда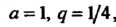, поэтому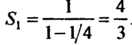Для второго ряда

Поэтому

Следовательно, сумма исходного ряда

Пример 23.25. Найти сумму ряда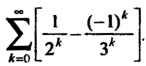 Данный ряд является разностью двух сходящихся геометрических рядов:

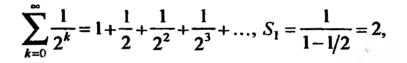
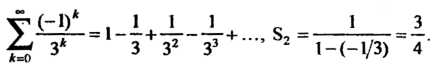
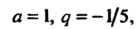
Значит исходный ряд имеет сумму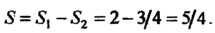

< Предыдущая		Следующая >