23.4. Знакопеременные ряды
Ряд, содержащий как положительные, так и отрицательные члены, называется знакопеременным. Знакопеременный ряд
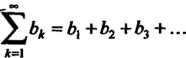
(23.20)
Сходится, если сходится рад, составленный из модулей его членов, т. е. ряд
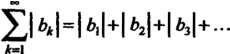
(23.21)
Ряд (23.20) в этом случае называется абсолютно сходящимся. Сумма абсолютно сходящегося ряда не зависит от порядка слагаемых.
Если рад (23.20) сходится, а ряд (23.21) расходится, то рад (23.20) называется условно (неабсолютно) сходящимся. Сумму условно сходящегося ряда путем перестановки его членов можно сделать равной любому данному числу, конечному или равному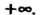
Ряд (23.21) является рядом с положительными членами, поэтому для исследования вопроса о его сходимости можно применять ранее рассмотренные признаки (признаки сравнения, интегральный признак, признак Коши, Д’Аламбера и др.).
Замечание 1.Из расходимости рада (23.21) в общем случае не следует расходимость ряда (23.20).
Рад, У которого любые два соседних члена имеют разные знаки, называется знакочередующимся.
Теорема 23.12 (признак Лейбница). Знакочередующийся ряд
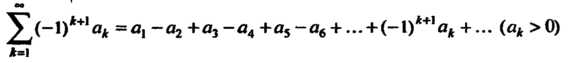
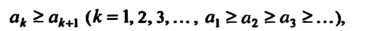 (23.22)
(23.22)
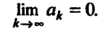 (23.23)
(23.23)
При замене суммы сходящегося знакочередующегося ряда суммой п его первых членов ошибка не превышает абсолютного значения первого т отброшенных членов, т. е.
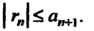 (23.24)
(23.24)
Теорема 23.13 (признак Дирихле). Знакопеременный ряд
(23.25)
Сходится, если: 1) частные суммы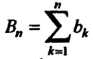 Ограничены, т. е.
Ограничены, т. е.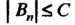
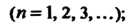 2) числа
2) числа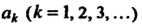 Образуют монотонную последователь
Образуют монотонную последователь
Ность, стремящуюся к нулю.
Замечание 2. Признак Лейбница является частным случаем признака Дирихле. В самом деле, если ак, монотонно убывая, стремится к нулю, а
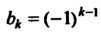 , то ряд (23.25) принимает вид
, то ряд (23.25) принимает вид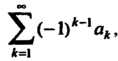 Для которого выполне
Для которого выполне
Ны условия признака Лейбница.
Теорема 23.14 (признак Абеля). Ряд (23.25) сходится, если: 1) сходится
Ряд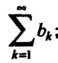 ; 2) числа
; 2) числа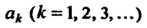 Образуют монотонную и ограниченную
Образуют монотонную и ограниченную
Последовательность.
Пример 23.18. Исследовать сходимость знакопеременного ряда
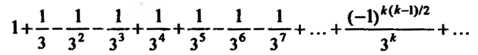
Составляем ряд из модулей членов данного ряда:

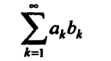
Последний ряд сходится, как геометрический ряд со знаменателем Следовательно, данный ряд также сходится; он является абсолютно сходящимся рядом (в соответствии с определением абсолютной сходимости ряда).

Пример 23.19. Исследовать сходимость ряда Составим ряд из модулей членов данного ряда:
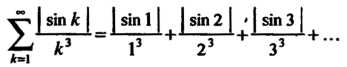
Так как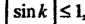 , то каждый член не превосходит соответствующего члена
, то каждый член не превосходит соответствующего члена
Сходящегося ряда
(ряд (2) является рядом Дирихле, т. е. рядом ввда (23.13), где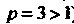 ). Согласно
). Согласно
Первому признак сравнения ряд (1) сходится, поэтому сходится и данный ряд, причем абсолютно.
Пример 23.20. Исследовать характер сходимости знакочередующегося рада
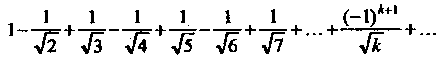
Поскольку ряд, составленный из модулей членов данного ряда, т. е. ряд расходится (ряд Дирихле;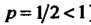 ), то о сходимости ряда пока ничего
), то о сходимости ряда пока ничего
Нельзя сказать (см. замечание 1). Применим к данному знакочередующемуся ряду признак Лейбница. Условия признака Лейбница здесь выполнены:
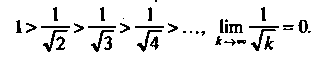
Следовательно, этот ряд сходится. Так как ряд из модулей расходится, то данный ряд сходится условно (неабсолютно).
Пример 23.21. Сколько нужно взять членов ряда
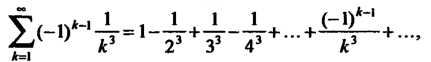
Чтобы вычислить его сумму с точностью до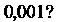
Данный ряд является знакочередующимся рядом, удовлетворяющим условиям признака Лейбница
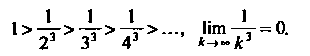
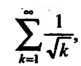
Следовательно, данный ряд сходится, причем абсолютно, так как ряд
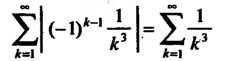
Является сходящимся (ряд Дирихле;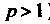 ).
).
Чтобы вычислить сумму ряда с указанной точностью, необходимо найти такой член, абсолютная величина которого меньше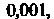 Т. е.
Т. е.
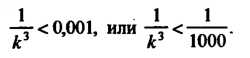
I Цследнее неравенство вьшолняется, когда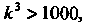 Или
Или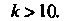 Следова
Следова
Тельно. нужно взять 10 членов данного ряда. Так как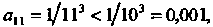 То
То
По формуле (23.24) получаем следующую оценку для остатка ряда: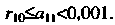
Пример 23.22. Исследовать характер сходимости ряда
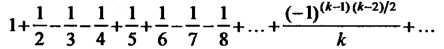
Ряд, составленный из модулей членов данного ряда, является гармоническим рядом, который расходится. Сравнение данного ряда с гармоническим не решает вопрос о его сходимости (см. замечание 1).
Применим признак Дирихле. Данный ряд можно представить в виде
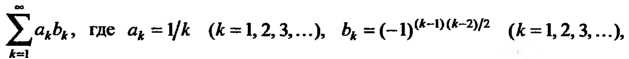
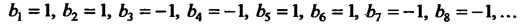
Поскольку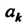 Монотонно стремится к нулю
Монотонно стремится к нулю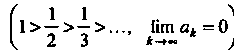 J, ча
J, ча
Стные суммы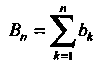 Ограничены
Ограничены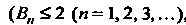 , ибо
, ибо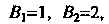
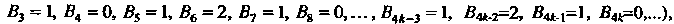
То, согласно признаку Дирихле, ряд сходится. Так как ряд из модулей его членов расходится, то данный ряд сходится условно (неабсолютно).
Пример 23.23. Доказать сходимость ряда

Применим признак Абеля. Этот ряд можно записать в виде
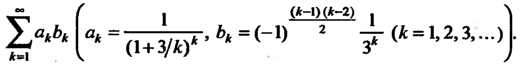
F)
Поскольку ряд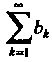 Сходится ибо сходится ряд
Сходится ибо сходится ряд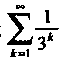 I, а числа ак образуют
I, а числа ак образуют
Монотонную ограниченную последовательность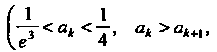
Так как
То, согласно признаку
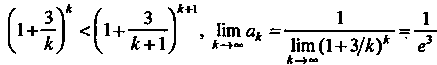 \
\
Абеля, данный ряд сходится.
| < Предыдущая | Следующая > |
|---|