23.3. Признак Д’Аламбера. Признак Коши. Другие признаки

Рассмотрим числовой ряд с положительными членами

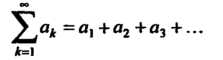(23.15)

Теорема 23.7 (признак Д’Аламбера). Пусть дляряда (23.15) существует

Если q< 1, то ряд (23.15) сходится; если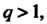То ряд расходится.

Замечание. Если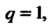Вопрос о сходимости ряда остается открытым. Теорема 23.8 (признак Коши). Пусть для ряда (23.15) существует

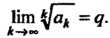(23.17)

Если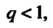То ряд сходится; если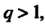То ряд расходится.

Теорема 23.9 (признак Раабе). Пусть для ряда (23.15) существует

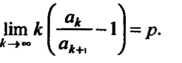
Если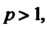То ряд сходится; если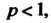То ряд расходится.

Теорема 23.10 (признак Г аусса). Пусть для ряда (23.15)

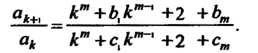
Если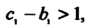То ряд сходится; если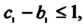То ряд расходится.

Пример 23.14. Доказать сходимость ряда

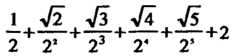
Общий член ряда определяется формулой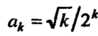. Заменяя в этой форму

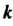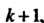ЛеНа. получаем последующий член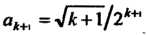. Составим отноше

Ние последующего члена к предыдущему:

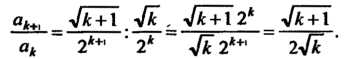
(23.19)

Найдем предел (23.16):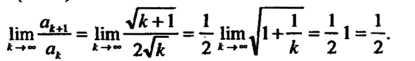

Так как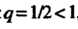, то на основании признака Д’Аламбера заключаем, что рад сходится.

Пример 23.15. Доказать сходимость ряда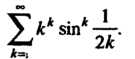

Применяем признак Коши. Поскольку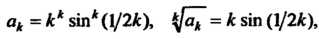 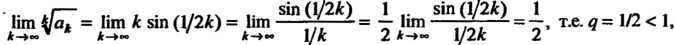 то ряд сходится.

Замечание. Сходимость данного ряда также можно установить с помощью признака Д’ Аламбера.

Пример 23.16. Исследовать, сходится или расходится ряд

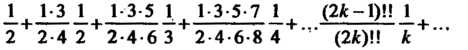
Общий член данного ряда определяется формулой

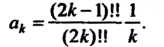
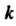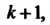Заменяя в этой формулеНаПолучаем формулу

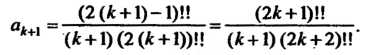
Составляем отношение последующего члена к предыдущему:

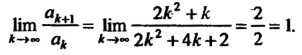
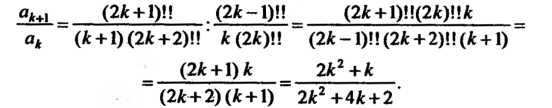
Находим предел (23.16):

Поскольку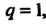То признак Д’Аламбера не дает ответа на вопрос о сходимости ряда. Обратимся к признаку Раабе. Найдем предел (23.18):

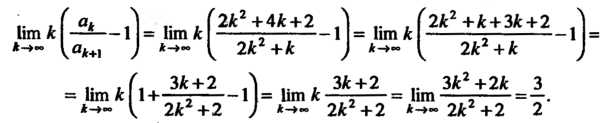
Так как в данном случае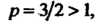То на основании признака Раабе заключаем,

Что ряд сходится.

Пример 23.17. Исследовал, условия сходимости гипергеометрическото ряда

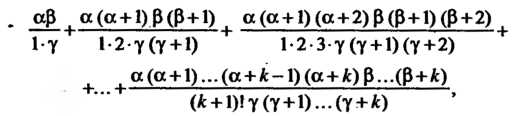
Где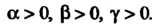1

Общий член данного ряда определяется формулой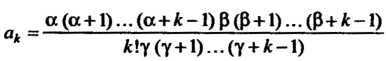

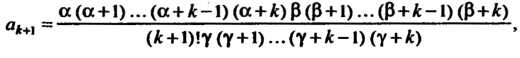
То

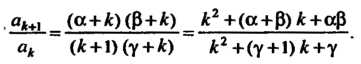
Из последнего выражения видно, что применение к данному ряду признака

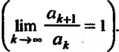
Д’Аламбера не дает ответа на вопрос о сходимости

Применим признак Гаусса. Так как в данном случае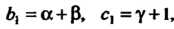То при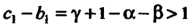Ряд сходится, при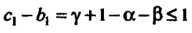Ряд расходится. Преобразуя полученные неравенства, заключаем, что ряд  сходится при 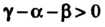И расходится при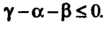

< Предыдущая		Следующая >