23.2. Ряды с положительными членами. Признаки сходимости. Признаки сравнения. Интегральный признак Коши

Рассмотрим числовые ряды с положительными членами:

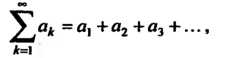(23.6)

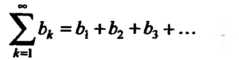(23.7)

Теорема 23.4 (первый признак сравнения). Если для всех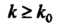

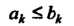(23.8)

И ряд (23.7) сходится, то сходится и ряд (23.6).

Если для всех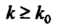

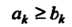(23.9)

И ряд (23.7) расходится, то расходится и ряд (23.6).

Теорема 23.5 (второй признак сравнения). Если существует конечный и отличный от нуля предел

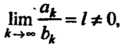(23.10)

То ряды (23.6) и (23.7) сходятся или расходятся одновременно.

Теорема 23.6 (интегральный признак Коши). Если-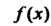

Неотрицательная невозрастающая функция при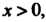То ряд

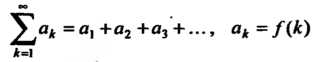(23.11)

Сходится или расходится одновременно с интегралом

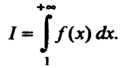(23.12)

Замечание. Нижним пределом интегрирования в интеграле (23.12) может быть любое другое положительное число из области определения функции /(х). Пример 23.6. Выяснить, сходится или расходится ряд

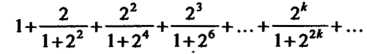
Все члены данного ряда положительны, общий член определяется формулой 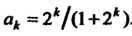. Сравним данный ряд с геометрическим рядом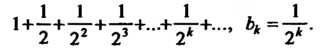

Так как

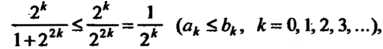
Т. е. выполнено условие (23.8) и ряд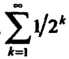Сходится (геометрический ряд, для

Которого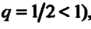, то на основании первого признака сравнения заключаем,

Что исходный ряд также сходится.

Пример 23.7. Выяснить, сходится или расходится ряд

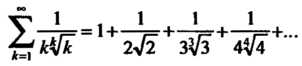
Сравним данный ряд с расходящимся гармоническим рядом (23.5).

Поскольку

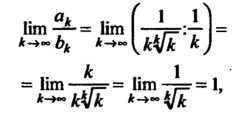
Т. е. выполнено условие (23.10), то из расходимости гармонического ряда следует расходимость данного ряда.

Пример 23.8. С помощью интегрального признака Коши доказать сходимость ряда

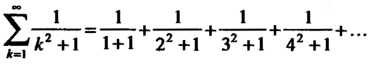
Рассмотрим функцию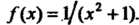Эта функция удовлетворяет условиям

Интегрального признака Коши: она принимает положительные значения и убывает с возрастанием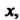Причем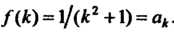Исследуем сходимость интеграла

(23.12) для данного случая:

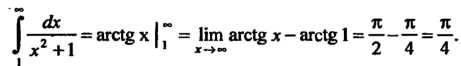
Так как интеграл сходится, то сходится и данный ряд.

Пример 23.9. С помощью интегрального признака Коши исследовать,

Сходится или расходится ряд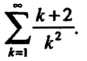

Функция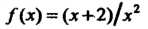Удовлетворяет условиям теоремы 23.6.

Т. е. интеграл расходится, то расходится и данный ряд.

Пример 23.11. Исследовать, при каких р сходится ряд Дирихле

(23.13)

Если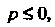То общий член ряда не стремится к нулю,По

Этому ряд расходится (на основании следствия из необходимого признака сходимости). В случае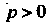Применим интегральный признак Коши. Функция

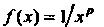Положительна и не возрастает при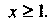Пусть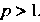Положив

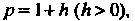Получим

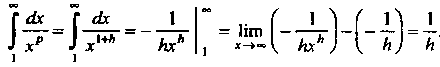
Т. е. интеграл вида (23.12) расходится, то расходится и данный ряд.

Пр и мер 23.10. Исследовать, сходится или расходится данный ряд

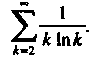
Применим интегральный признак, рассмотрим функцию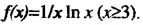Так как

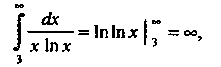
Поскольку интеграл вида (23.12) сходится, то сходится и ряд Дирихле. Если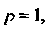То

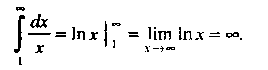
Интеграл расходится, поэтому расходится и ряд Дирихле (при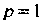Получаем гармонический ряд).

Итак, ряд Дирихле сходится при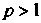И расходится при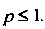

Замечание. Сходимость многих рядов может быть исследована сравнением с соответствующим рядом Дирихле. Вопрос о сходимости ряда

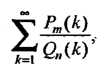(23.14)

Где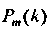И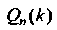- многочлены от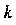Степен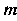иИ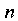Соответственно, решается

Сравнением с рядом Дирихл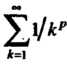е, где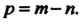При этом целесообразно

Применять второй признак сравнения.

П р и м е р 23.12. Доказать сходимость ряда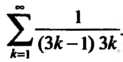 Преобразуем формулу для общего члена данного ряда:

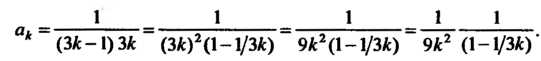
Рассмотрим ряд с общим членом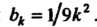Ряд

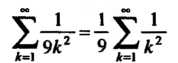
Сходится, ибо это ряд вида (23.13), где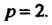Так как

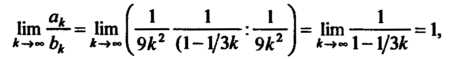
Т. е. выполнено условие (23.10), то данный ряд также сходится.

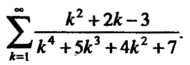
Пример 23.13. Исследовать сходимость ряда

Это ряд вида (23.14), причем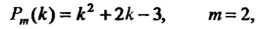

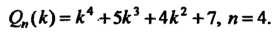Так как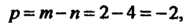Сравним данный

Ряд с рядом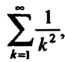Который является рядом Дирихле и сходится, ибо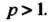

Поскольку

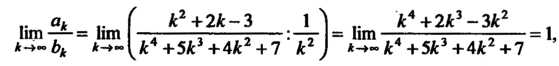
Т. е. выполнено условие (23.10), то данный ряд сходится.

< Предыдущая		Следующая >