23.1. Основные понятия. Необходимый признак сходимости

Рядом называется выражение вида

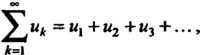
Где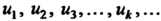- последовательность чисел или функций. Слагаемые

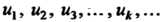Называются членами ряда. Если все члены ряда являются числами, то ряд называется числовым., если члены ряда — функции, то ряд называется функциональным.

Рассмотрим числовой ряд

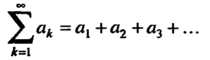
(23.1)

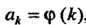
Ряд (23.1) задан, если известен его общий член  , т. е. известно правило,

По которому каждому номеру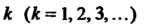Ставится в соответствие вполне

Определенный член ряда.

Суммой конечного числа п первых членов ряда называется его п-й частичной суммой:

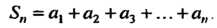
Конечный или бесконечный предел частичной суммы приНазывается

Суммой ряда:

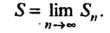
Ряд, имеющий конечную сумму, называется сходящимся. Если ряд (23.1) сходится и его сумма равна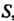, то используют запись

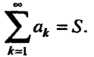
Если предел частичной суммы не существует или бесконечен, то ряд называется расходящимся.

Ряд, члены которого неотрицательны, называется положительным. Положительный ряд всегда имеет сумму; эта сумма будет конечной (и, следовательно, ряд

- сходящимся), если его частичные суммы ограничены сверху, и бесконечной (а ряд - расходящимся), если суммы сверху не ограничены.

Если в ряде (23.1) отбросить первые т членов, то получится ряд

Называемый остатком ряда (23.1) после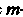-го члена.

Теорема 23.1. Если сходится ряд (23.1), то сходится и любой из его остатков (23.2); обратно, их сходимости остатка (23.2) вытекает сходимость исходного ряда (23.1).

Теорема 23.2. Если ряд (23.1) сходится, то сумма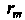Его остатка (23.2) после т-го члена с возрастанием т стремится к нулю: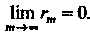

Теорема 23.3 (необходимый признак сходимости). Если ряд (23.1) сходится, то его общий член стремится к нулю, те.

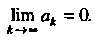(23.3)

Следствие. Если общий член ряда к нулю не стремится, то ряд расходится. Примеры числовых рядов: геометрический ряд

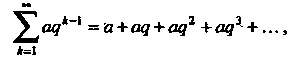
(23.4)

Гармонический ряд

(23.5)

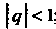
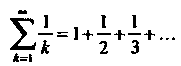
Отметим, что геометрический ряд сходится тогда и только тогда, когда ;

Его сумма определяется формулой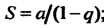; гармонический ряд расходится.

Замечание. Условие (23.3) не является достаточным для сходимости ряда (23.1).

Пример 23.1. Найти сумму ряда

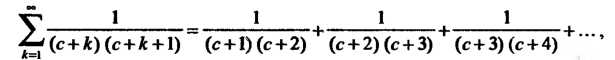
Где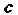- постоянная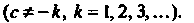

Составим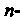Ю сумму данного ряда:

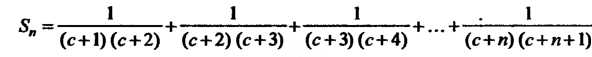
Чтобы упростить выражение для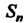, преобразуем формулу общего члена ряда, разлагая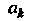На элементарные дроби. Положим

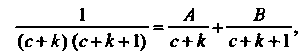
Отсюда

Сравнивая коэффициенты при одинаковых степенях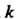В числителях обеих частей равенства, получаем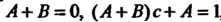, откуда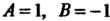, поэтому

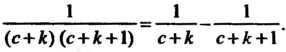
Выражение для принимает вид

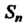
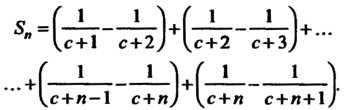
Приводя подобные члены и переходя к пределу, получаем 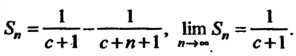 Следовательно,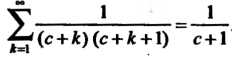

Замечание. В частных случаях при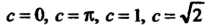По этой

Формуле получаем соответственно:

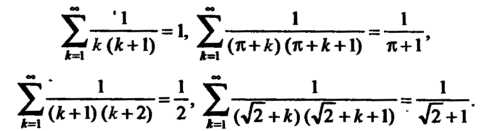
Г

Пример 23.2. Найти сумму ряда 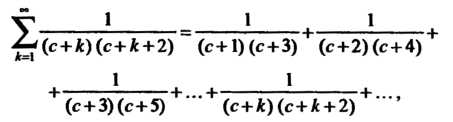 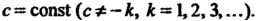 Разложив общий член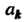На элементарные дроби, получим

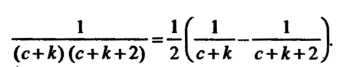
В частном случае при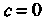Находим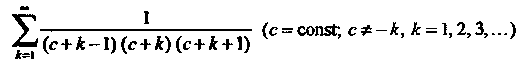 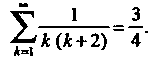  Пример 23.3. Найти сумму ряда Разлагая общий член ряда на элементарные дроби, получаем

Составим п-ю частичную сумму данного ряда и преобразуем ее:

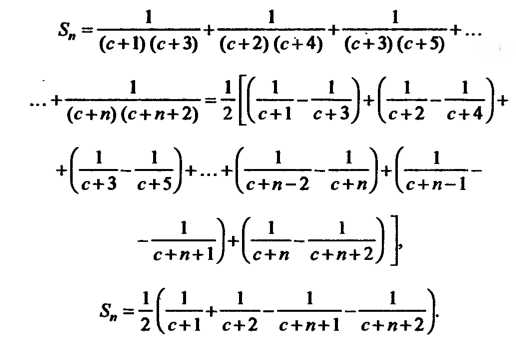
Следовательно,

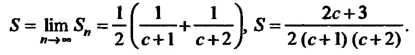
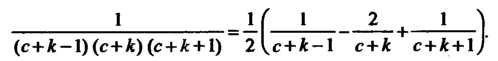
Составляя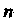-ю частную сумму и преобразуя ее, находим

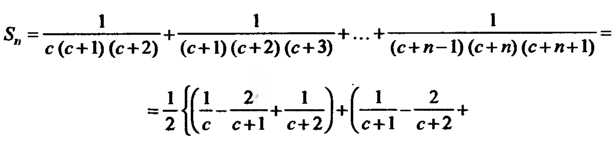
Следовательно,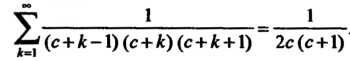

В частности, при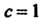Из последней формулы находим

Л.

Пример 23.4. Выяснить, сходится или расходится ряд

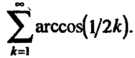
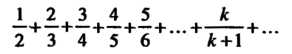
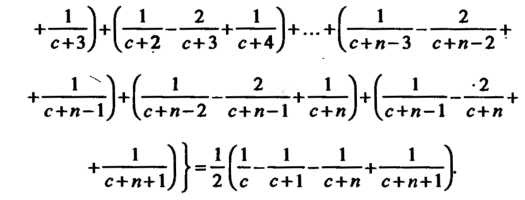
Переходя к пределу, получаем

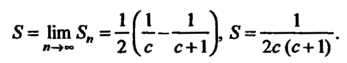
Общий член ряда выражается формулой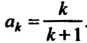Так как

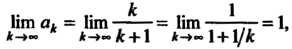Т. е. общий член к нулю не стремится, то на

Основании следствия из необходимого признака заключаем, что данный ряд расходится.

Пример 23.5. Исследовать, сходится или расходится ряд

Общий член ряда определяется формулой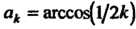Так как

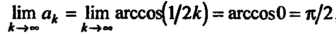, т. е. предел общего члена не равен

Нулю, то на основании следствия из необходимого признака сходимости заключаем, что данной ряд расходится.

< Предыдущая		Следующая >