22.4. Приложения интегралов по поверхности

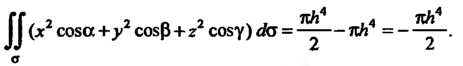
ПлощадьПоверхностиВычисляется по формуле

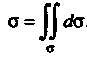(22.13)

Если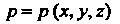- поверхностная плотность массы материальной поверх

Ности (о), то масса всей этой поверхности определяется интегралом

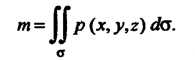
(22.14)

Координаты центра тяжести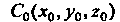Поверхности о вычисляются по

Формулам

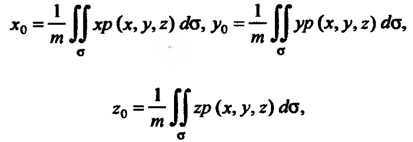
(22.15)

Где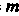Определяется формулой (22.14).

Моменты инерции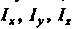Относительно координатных осей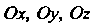На

Ходятся соответственно по формулам

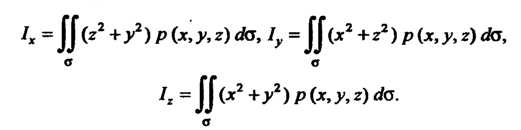
Моменты инерции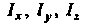Относительно координатных плоскостей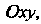

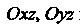Вычисляются соответственно по формулам

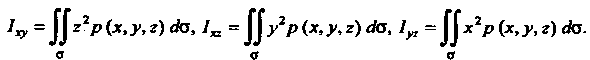(22.17)

Пример 22.9. Вычислить массу части поверхности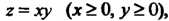 вырезанной цилиндром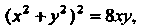Если поверхностная плотность

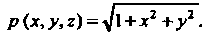
Так как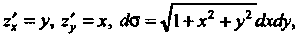То

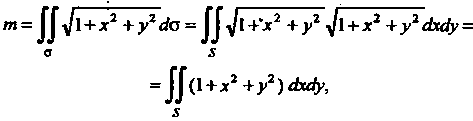
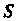
Где — лепесток лемнискаты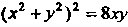, для которого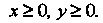

В полярных координатах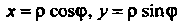Уравнение границы области

Имеет вид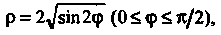Поэтому

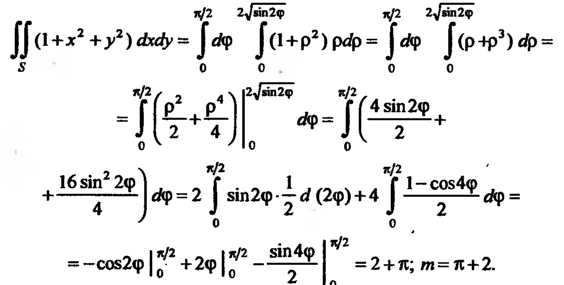
Пример 22.10. Найти массу части цилиндрической поверхности 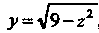, отсеченной плоскостями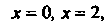Если поверхностная

Плотность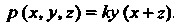

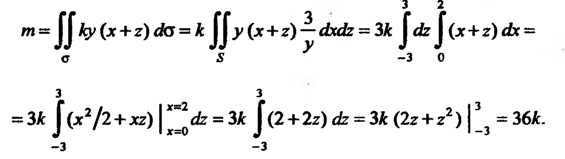
Пример 22.11. Вычислить момент инерции относительно оси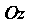Части однородной поверхности сферы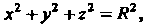Для которой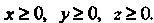

Так как поверхность однородная, т. е.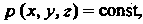То в формулах (22.16)

Можно положить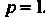

Третья из формул (22.16) принимает вид

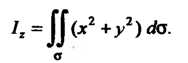
Поскольку в данном случае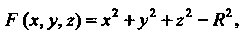

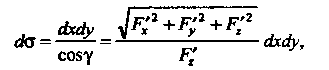
То

Следовательно,

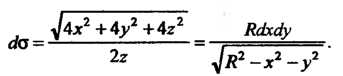
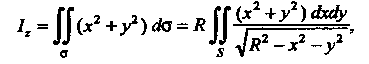
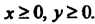
Где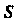- четверть круга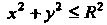При

Переходя к полярным координатам получаем

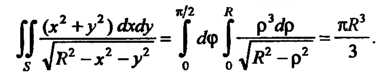
(Последний интеграл вычислен с помощью подстановки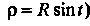. Итак,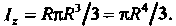

Гпава 23

ЧИСЛОВЫЕ РЯДЫ

< Предыдущая		Следующая >