22.3. Формула Стокса. Формула Остроградского
Если функции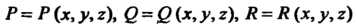 Непрерывно диффе
Непрерывно диффе
Ренцируемы и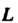 - замкнутый кусочно-гладкий контур, ограничивающий конечную кусочно-гладкую двустороннюю поверхность о, то справедлива формула Стокса
- замкнутый кусочно-гладкий контур, ограничивающий конечную кусочно-гладкую двустороннюю поверхность о, то справедлива формула Стокса
(22.11)
Где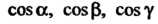 - направляющие косинусы нормали к поверхности
- направляющие косинусы нормали к поверхности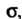
Причем направление нормали определяется так, чтобы со стороны нормали обход контура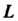 Совершался против часовой стрелки (в правой системе координат). Формула Стокса может быть записана в следующем символическом виде:
Совершался против часовой стрелки (в правой системе координат). Формула Стокса может быть записана в следующем символическом виде:
Если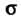 - кусочно-гладкая поверхность, ограничивающая объем
- кусочно-гладкая поверхность, ограничивающая объем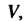 И
И
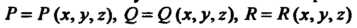 - функции, непрерывные вместе со
- функции, непрерывные вместе со
Своими частными производными первого порядка в области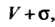 То справедли
То справедли
Ва формула Остроградского
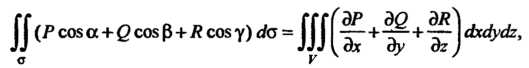 (22.12)
(22.12)
Где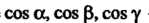 - направляющие косинусы внешней нормали к поверхности о.
- направляющие косинусы внешней нормали к поверхности о.
Пример 22.7. С помощью формулы Стокса вычислить криволинейный
Интеграл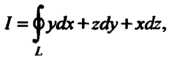 Где
Где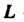 - окружность
- окружность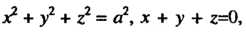
Пробегаемая против часовой стрелки, если смотреть с положительной стороны оси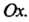 В данном примере
В данном примере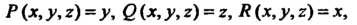 Поэтому
Поэтому
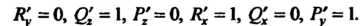
По формуле (22.11) имеем
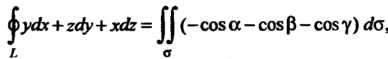
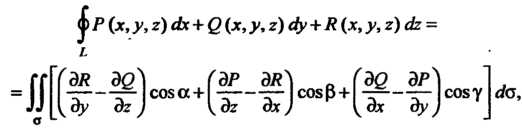
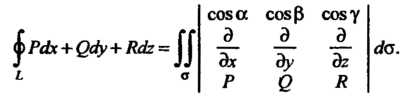
Где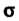 - часть плоскости
- часть плоскости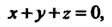 Ограниченная данной окружностью. При
Ограниченная данной окружностью. При
Водя уравнение плоскости,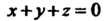 К нормальному виду, находим
К нормальному виду, находим 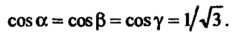
Таким образом,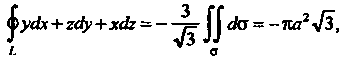 Где
Где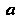 — радиус кру
— радиус кру
Га, ограниченного указанной окружностью.
Пример22.8. С помощью формулы Остроградского вычислить
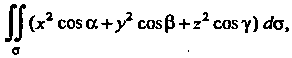 Где
Где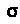 — часть конической поверхности
— часть конической поверхности 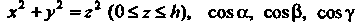 — направляющие косинусы внешней
— направляющие косинусы внешней
Нормали к этой поверхности.
Чтобы решить задачу, достаточно вычислить второй и третий интегралы. В случае области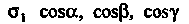 — косинусы углов с осями координат нор
— косинусы углов с осями координат нор
Мали к плоскости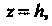 А именно:
А именно: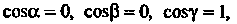 Поэтому
Поэтому
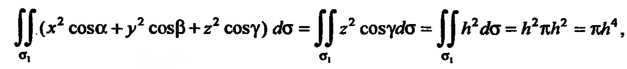
— направляющие косинусы внешней
Нормали к этой поверхности.
Формула Остроградского применима в случае замкнутой поверхности. Чтобы получить замкнутую поверхность, присоединим к поверхности конуса соответствующую часть плоскости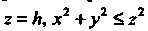 . Обозначив эту часть плоскости через, по формуле Остроградского получим
. Обозначив эту часть плоскости через, по формуле Остроградского получим
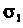
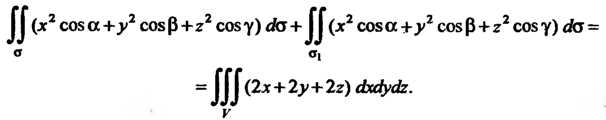
Так как на плоскостк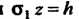 И двойной интеграл равен площади круга радиуса
И двойной интеграл равен площади круга радиуса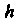 ,
,
Получающегося при пересечении конуса с плоскостью.
Вычисляем третий интеграл, производя в нем сначала интегрирование по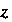 От
От
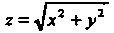 До
До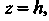 А затем двойной интеграл по области
А затем двойной интеграл по области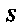 В плоскости
В плоскости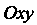
(эта область является кругом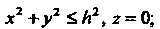 Она получается проецированием
Она получается проецированием
Объема На плоскость
На плоскость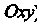 |.
|.
Таким образом,
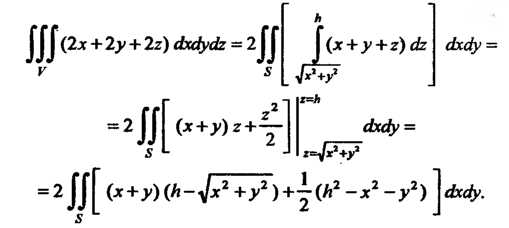
Обозначая последний интеграл через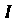 И переходя к полярным координатам по формулам
И переходя к полярным координатам по формулам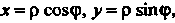 Находим
Находим
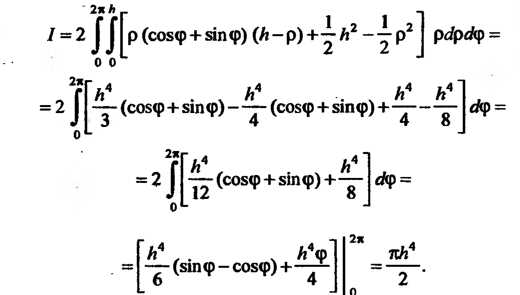
Итак,
| < Предыдущая | Следующая > |
|---|