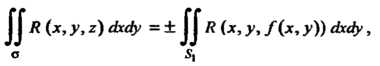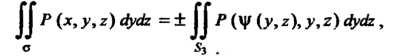22.2. Поверхностные интегралы второго рода
Пусть в точках двусторонней поверхности Задана непрерывная функция
Задана непрерывная функция 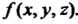 Выберем на поверхности определенную сторону. Разобьем поверхность
Выберем на поверхности определенную сторону. Разобьем поверхность 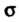 Сетью произвольно проведенных кривых на части
Сетью произвольно проведенных кривых на части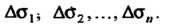
В каждой части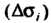 Выберем по произ
Выберем по произ
Вольной точке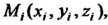 Вычислим в ней
Вычислим в ней
Значение данной функции. Это значение 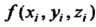 Умножим на проекцию
Умножим на проекцию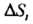 Части
Части 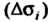 На плоскости
На плоскости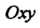 (а не на площадь
(а не на площадь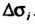 как это было в случае интеграла первого рода). При этом числу
как это было в случае интеграла первого рода). При этом числу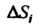 Приписывается определенный знак, а именно если в точках
Приписывается определенный знак, а именно если в точках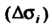 Нормаль, отвечающая выбранной стороне поверхности составляет с осью
Нормаль, отвечающая выбранной стороне поверхности составляет с осью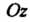 Острый угол, то через
Острый угол, то через 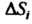 Обозначаем площадь проекции
Обозначаем площадь проекции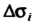 , взятую со знаком плюс, если упомянутая нормаль составляет с осью
, взятую со знаком плюс, если упомянутая нормаль составляет с осью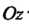 Тупой угол, то под
Тупой угол, то под 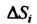 Будем понимать площадь этой проекции, взятую со знаком минус. Составим сумму всех таких произведений:
Будем понимать площадь этой проекции, взятую со знаком минус. Составим сумму всех таких произведений:
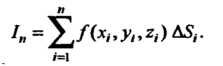
Интегралом второго рОда от функции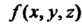 По поверхности
По поверхности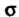 Называется
Называется
Предел суммы (22.6) при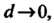 Где
Где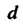 - наибольший из диаметров
- наибольший из диаметров
Элементарных областей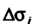 :
:
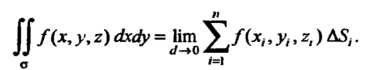
Где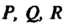 - функции от
- функции от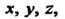 Определенные и непрерывные в точках двусто
Определенные и непрерывные в точках двусто
Ронней поверхности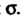
Интеграл второго рода обладает всеми свойствами интеграла первого рода за исключением одного: при изменении стороны поверхности интеграл (22.7) меняет знак. Интегралы первого и второго рода связаны формулой
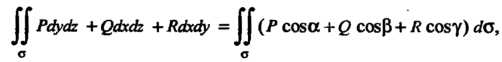
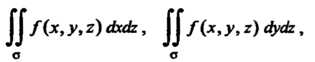
Причем для выбора знака проекции элемента служит угол между нормалью, отвечающей выбранной стороне, и осью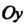 Или
Или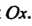
Наиболее общим видом интеграла второго рода служит интеграл
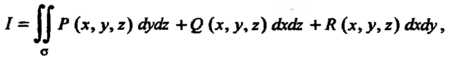
Где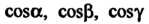 - направляющие косинусы нормали, направленной в ту
- направляющие косинусы нормали, направленной в ту
Сторону поверхности, по которой берется интеграл второго рода.
Интегралы второго рода вычисляются следующим образом. Если поверхность а однозначно проецируется в область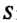 Плоскости
Плоскости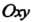 И
И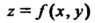 - ее уравнение, то
- ее уравнение, то
Где знак плюс берется в том случае, когда на выбранной стороне поверхности 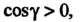 И знак минус, когда
И знак минус, когда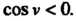 Аналогично, если
Аналогично, если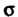 Однозначно проеци
Однозначно проеци
Руется в область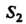 (или
(или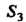 ) на плоскости
) на плоскости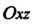 (или
(или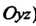 I, т. е. может быть задана уравнением
I, т. е. может быть задана уравнением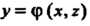 (или
(или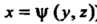 ), то
), то
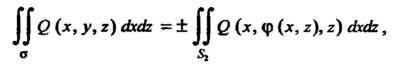 (22.9)
(22.9)
Где в случае (22.9) берется знак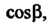 А в случае (22.10) - знак
А в случае (22.10) - знак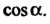
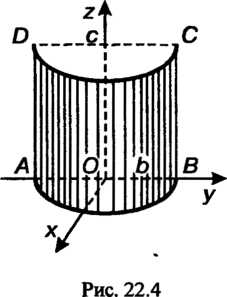
Пример 22.4. Вычислить поверхностный интеграл второго рода 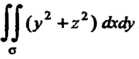 , где
, где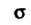 — верхняя сторона поверхности
— верхняя сторона поверхности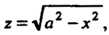
Нормаль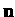 В точке
В точке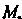 . соответствующая указанной стороне поверхности, составляет с осью
. соответствующая указанной стороне поверхности, составляет с осью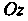 Острый угол (точнее
Острый угол (точнее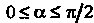 ), поэтому в формуле (22.8), которой следует воспользоваться, нужно взять знак плюс. Проекцией
), поэтому в формуле (22.8), которой следует воспользоваться, нужно взять знак плюс. Проекцией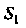 Данной поверхности на плоскость
Данной поверхности на плоскость Является прямоугольник
Является прямоугольник (рис. 22.5, б), определяемый неравенствами
(рис. 22.5, б), определяемый неравенствами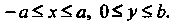 По формуле (22.8) находим
По формуле (22.8) находим
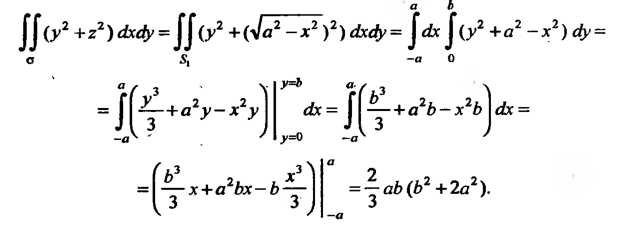
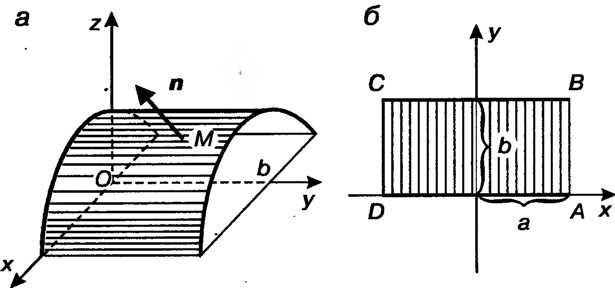
Пример 22.5. Вычислить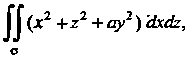 Где
Где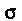 - внешняя сторо
- внешняя сторо
На поверхности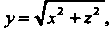 Отсеченной плоскостями
Отсеченной плоскостями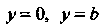 (см. рис. 22.3).
(см. рис. 22.3).
Нормаль к поверхности в точке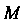 Образует с осью
Образует с осью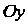 Тупой угол, поэтому в формуле (22.9) следует взять знак минус.
Тупой угол, поэтому в формуле (22.9) следует взять знак минус.
Проекцией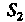 Данной поверхности на плоскость
Данной поверхности на плоскость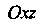 Является круг
Является круг
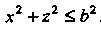 . По формуле (22.9) получаем
. По формуле (22.9) получаем
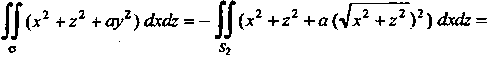
Следовательно,
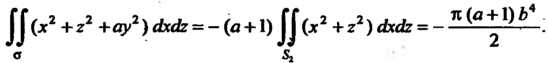
Пример 22.6. Вычислить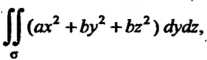 Где
Где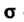 - внутренняя
- внутренняя
Сторона части полусферы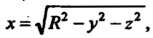 Вырезанная конусом
Вырезанная конусом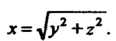
В формуле (22.10), которой воспользуемся, следует взять знак минус, так как нормаль, соответствующая выбранной стороне поверхности, составляет с положительным направлением оси Ох тупой угол:
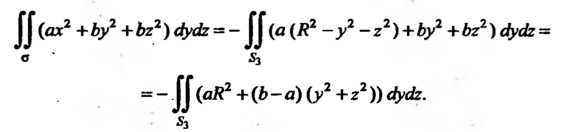
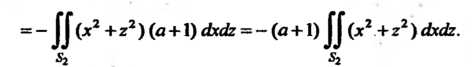
Переходя к полярным координатам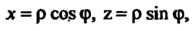 Находим
Находим
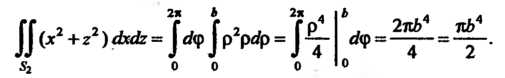
Так как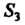 Есть круг
Есть круг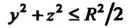 (получено из уравнений
(получено из уравнений
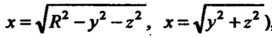 , то, переходя к полярным координатам, находим
, то, переходя к полярным координатам, находим
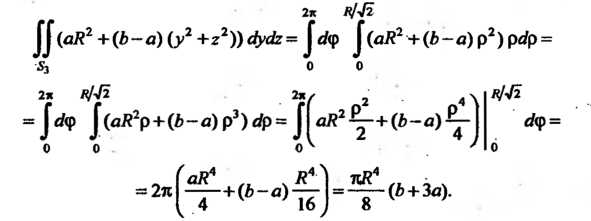
| < Предыдущая | Следующая > |
|---|