22.1. Поверхностные интегралы первого рода

Пусть дана функцияНепрерывная на некоторой гладкой поверхно

Сти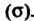Разобьем поверхность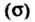Сетью произвольно проведенных кривых (рис. 22.1) на ряд частей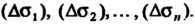В каждой из этих частей

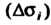Выберем произвольно одну точку 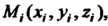Вычислим значение данной функции в этой точке и, умножив его на площадь соответствующей части поверхности, составим сумму всех таких произведений

(22.1)

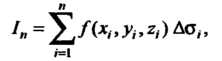
Называемую интегральной суммой. Обозначим через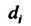Диаметр элементарной части поверхности-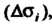

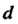Наибольший из указанных диаметров.

Интегралом первого рода от функции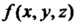По поверхности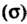Называет

Ся предел интегральной суммы (22.1) при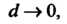Где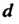- наибольший из

Диаметров области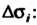

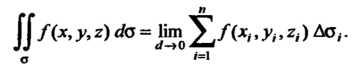
(22.2)

Интеграл первого рода обладает свойствами, аналогичными свойствам криволинейных интегралов первого рода.

Если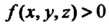И функцию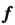Рассматривать как поверхностную плотность

Массы материальной поверхности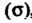, то интеграл (22.2) определяет массу этой поверхности.

Когда поверхность задана уравнением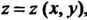Интеграл (22.2) вычисляется

По (honMVJie

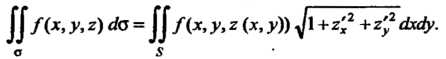
(22.3)

Если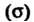— кусочно-гладкая двусторонняя поверхность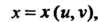

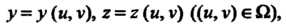А функция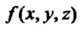Определена и непрерывна

В точках поверхности (о), то

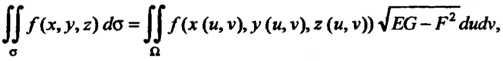(22.4)

Где

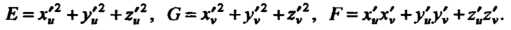(22.5)

Формула (22.3) является частным случаем формулы (22.4) при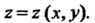

Пример 22.1. Вычислить поверхностныйинтеграл первого рода

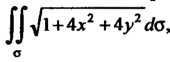Где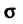- конечная часть

Поверхности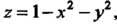Отсеченная плос

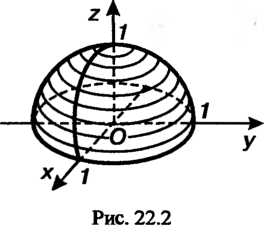
Костью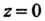(рис. 22.2).

Проекцией рассматриваемой части данного ¦ параболоида вращения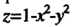На плоскость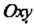

Является область, ограниченная окружностью 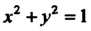(получено из уравнений поверхности и плоскости). Следовательно, областью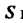В формуле (22.3) является круг 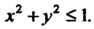Так как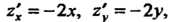То в соответствии с формулой (22.3) получаем

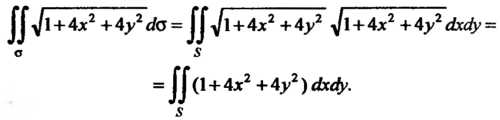
Для вычисления полученного двойного интеграла перейдем к полярным координатам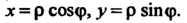Замечая, что в области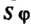Меняется от 0 до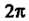И 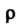- от 0 до 1, находим

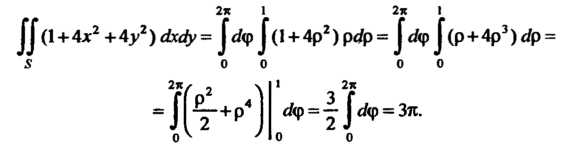
Пример 22.2. Вычислить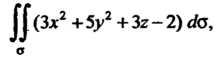Где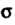- часть по

Верхности, отсеченной плоскостями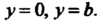

Поверхность задана уравнением, разрешенным относительно у. Для вычисления интеграла по поверхности первого рода воспользуемся формулой

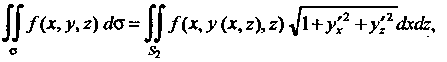
Где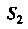— проекция поверхности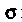На плоскость 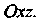Поскольку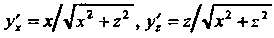, то

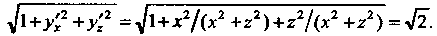
Проекцией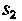Данной поверхности на плоскость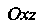Является круг

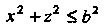(рис. 22.3), поэтому при переходе к полярным координатам 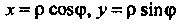Будем иметь По указанной формуле находим

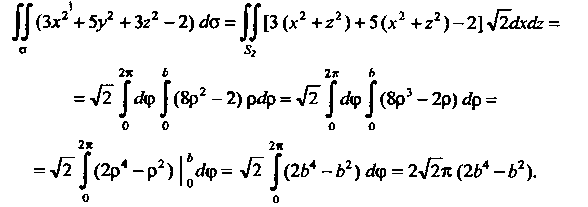
Пример 22.3. Вычислить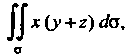Где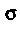— часть цилиндриче

Ской поверхности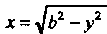, отсеченной плоскостями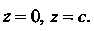

Так как поверхность задана уравнением, разрешенным относительно х, то необходимо воспользоваться формулой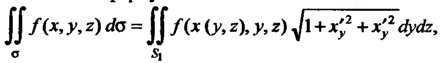

Где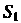- проекция поверхности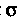На плоскость 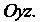Поскольку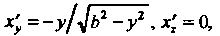То

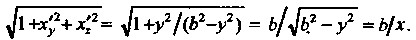
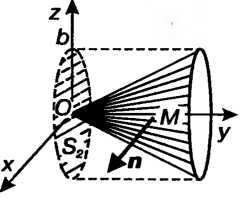
Заметив еще, что в данном случае область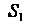Представляет собой

Прямоугольник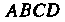(рис. 22.4), опреде

Ляемый неравенствами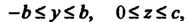 по указанной формуле найдем:

< Предыдущая		Следующая >