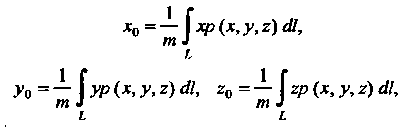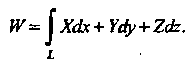21.4. Приложения криволинейных интегралов
Длина
Дуги
Плоской или пространственной линии вычисляется по формуле
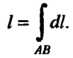
Если пространственная линия задана параметрическими уравнениями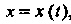
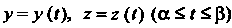, то
Площадь S фигуры, расположенной в плоскости Оху и ограниченной замкнутой линией L, находится по формуле
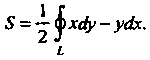(21.19)
Масса /я материальной дуги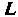
Определяется формулой
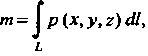(21.20)
Где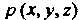
- линейная плотность вещества в точке_
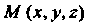Этой дуги.
Прямоугольные координаты центра тяжести материальной дуги находятся по формулам
Где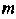
Определяется формулой (21.20).
Если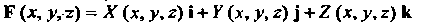
- переменная сила,
Совершающая работу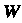
Адоль пути
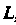, и функции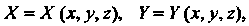
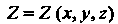Непрерывны, то
Пусть сила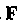
Имеет потенциал, т. е. существует функция
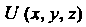Такая, что вы
Ражение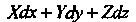
Является ее полным дифференциалом
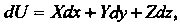Тогда работа независимо от пути L равна
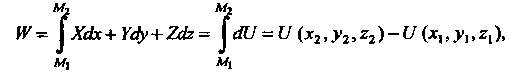
Где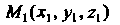
- начальная,
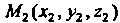- конечная точки пути.
Замечание. Если линия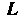
Лежит в плоскости
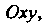То формулы
(21.18), (21.20) - (21.22) упрощаются.
Пример 21.13. Найти массу материальной дуги кривой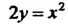
Между
Точками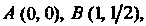
Если линейная плотность вещества в точке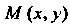
Пропорциональна абсциссе этой точки.
Найдем выражения линейной плотности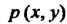
И дифференциала дуги. Из
Условия следует, что линейная плотность выражается формулой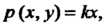
Где
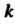- коэффициент пропорциональности. Из уравнения линии
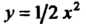Находим
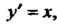Поэтому
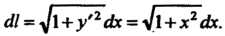Согласно формуле (21.20), имеем
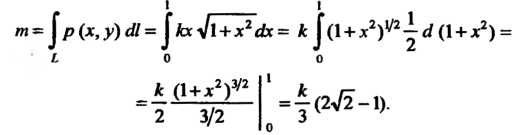
Пример 21.14 Найти центр тяжести дуги винтовой линии
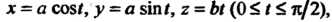Если линейная плотность в точке 
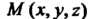Пропорциональна произведению первых двух координат.
Так как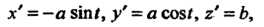
То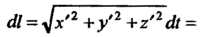
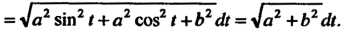
Согласно условию, линейная плотность выражается формулой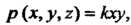
где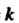
- коэффициент пропорциональности.
По формуле (21.20) находим массу данной дуги
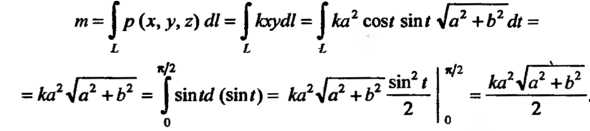
Итак,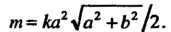
Вычислим интегралы каждой из формул (21.21), обозначив их через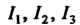
соответственно:
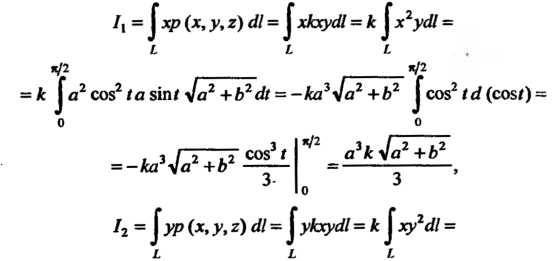
Таким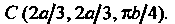
Образом, искомый центр тяжести находится в точке
Пример 21.15. Найти работу, производимую силой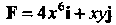
Вдоль
Дуги кривой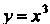
От точки
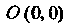До точки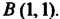
Проекции силы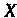
И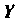
На координатные оси соответственно равны 
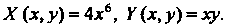Чтобы найти работу, необходимо воспользоваться частным случаем формулы (21.22):
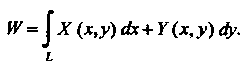
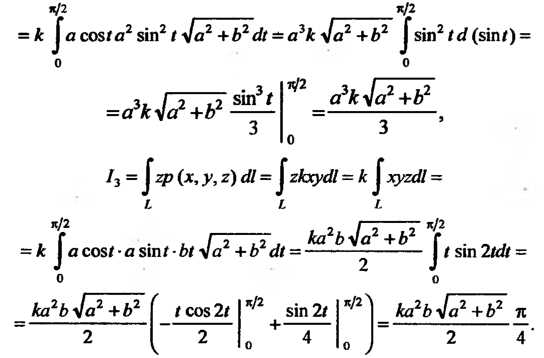
По формулам (21.21) находим координаты центра тяжести:
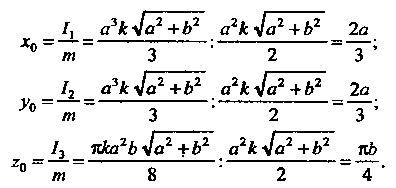
По этой формуле получаем
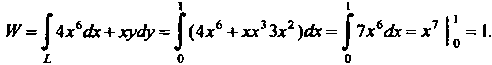
Гпава 22
| < Предыдущая | Следующая > |
|---|
