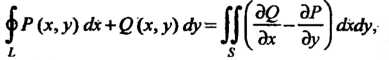21.3. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования

Если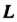- кусочно гладкий контур, ограничивающий на плоскости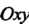1 область 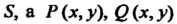- функции, заданные в замкнутой области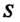И имеющие в ней непрерывные частные производные, то справедлива формула Грина

(21.12)

Где обход контура выбирается так, чтобы область S оставалась слева.

Криволинейный интеграл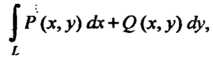Где контурЦеликом ле

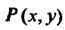Жит внутри односвязной областиВ которой функцииИ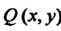I непре

Рывны вместе со своими частными производными, не зависит от пути интегрирования тогда и только тогда, когда

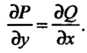(21.13)

В этом случае подынтегральное выражениепредставляет собой полный дифференциал некоторой функци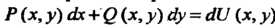иI и

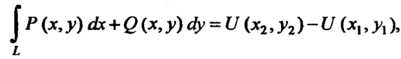(21.14)

Где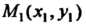- начальная,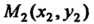- конечная точки пути интегрирования.

Криволинейный интеграл по замкнутому контуру в этом случае равен нулю:

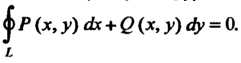
Криволинейный интеграл

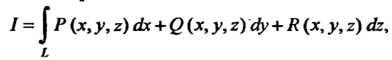(21.15)

Где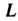- контур, целиком лежащий в односвязной области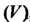, в которой функции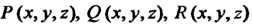Непрерывны вместе со своими частными производными, не зависит от пути интегрирования тогда и только тогда, когда выполняются равенства

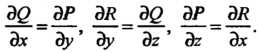(21.16)

В этом случае подынтегральное выражение представляет собой полный дифференциал некоторой функции: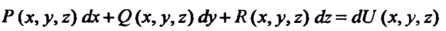

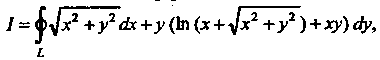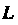Пример 21.11. С помощью формулы Грина вычислить криволинейный интеграл второго родаГде- контур

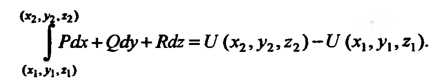
Криволинейный интеграл по замкнутомуКонтуру в таком случае равен нулю:

(21.17)

Прямоугольника с вершинами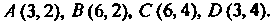

Преобразуем этот интеграл по формуле Грина. Поскольку

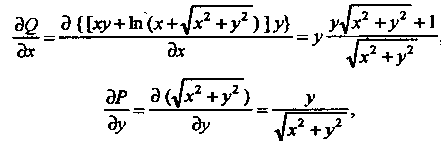
То по формуле (21.12) имеем

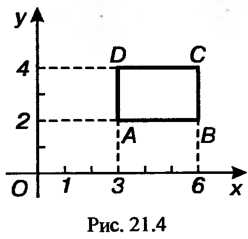
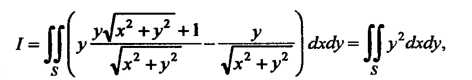
Где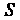- область, ограниченная контуром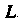, в данном  случае  прямоугольник

(рис. 21.4).

Вычисляем полученный двойной интеграл по прямоугольнику

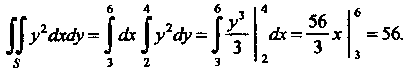
Пример 21.12. Вычислить криволинейный  интеграл  второго  рода

По путиС началом в точ

КеИ концом в точке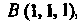, предварительно установив, что он не

Зависит от пути интегрирования.

Это интеграл вида (21.15), для которого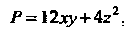

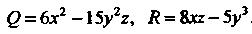
Так как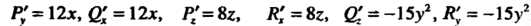. то

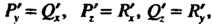Т. е. выполнены условия (21.16).

Следовательно, интеграл не зависит от пути интегрирования. Вычислим его по отрезку прямой, проходящей через точкиИПараметрические уравнения прямой имеют вид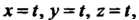Поэтому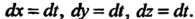Так как на отрезке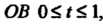То

Замечание. Этот пример можно решить и с помощью формулы

(21.17), Действительно, так как выполнены условия (21.16), то подынтегральное выражение является полным дифференциалом некоторой функции

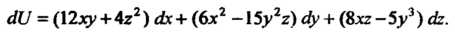
С другой стороны,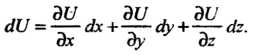

Сравнивая два выражения для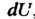, получаем

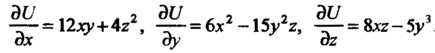
Из первого равенства, считая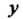И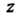Постоянными, находим

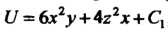; постоянная интегрированияЯвляется постоянной по отношению к, но она зависит отИ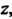, т. е.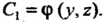

Итак,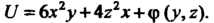Находя частную производную по у от функции

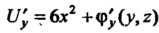И сравнивая с выражением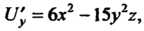Получаем

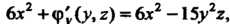Откуда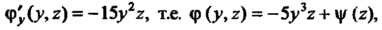

Поэтому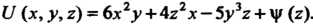

Поскольку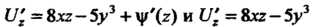, то, т. е.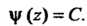

Следовательно,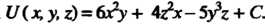По формуле (21.17) находим

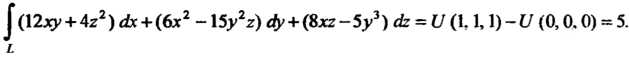
< Предыдущая		Следующая >