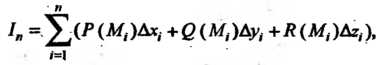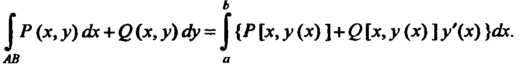21.2. Криволинейные интегралы второго рода
Пусть дана дуга пространственной кусочно-гладкой кривой, ограниченная точками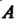 И
И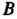 (см. рис. 21.1), и определенная на ней непрерывная вектор-функция
(см. рис. 21.1), и определенная на ней непрерывная вектор-функция
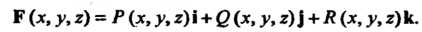 (21.7)
(21.7)
Дугу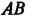 Разобьем на
Разобьем на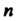 Элементарных дуг
Элементарных дуг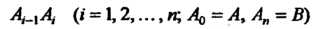
Точками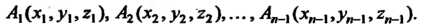 На каждой дуге
На каждой дуге
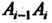 Выберем произвольно точку
Выберем произвольно точку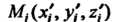 Значения функций в точке
Значения функций в точке
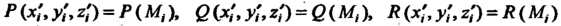 Умножим на
Умножим на
Проекции этой дуги соответственно на оси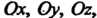 Которые обозначим через
Которые обозначим через
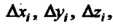 Причем
Причем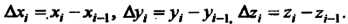 Из полученных
Из полученных
Произведений составим сумму
Называемую интегральной суммой по координатам для вектор-функции (21.7). Обозначим через Длину наибольшей из проекций
Длину наибольшей из проекций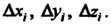
Криволинейным интегралом второго рода или криволинейным интегралом по координатам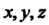 Называется предел интегральной суммы (21.8) при
Называется предел интегральной суммы (21.8) при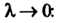
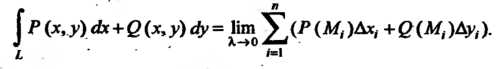
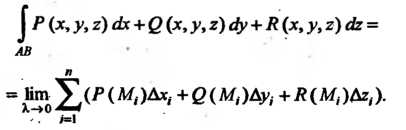
На кривой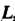 , целиком лежащей в плоскости
, целиком лежащей в плоскости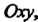 Функции
Функции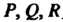 Не зависят от
Не зависят от
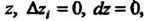 Поэтому
Поэтому
Если функции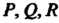 Рассматривать как проекции некоторой переменной силы
Рассматривать как проекции некоторой переменной силы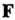
На координатные оси, то криволинейный интеграл второго рода выражает работу силы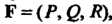 Точка приложения которой описывает кривую
Точка приложения которой описывает кривую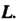
Криволинейный интеграл второго рода зависит от выбора направления обхода кривой; если изменить направление обхода, то интеграл меняет знак:
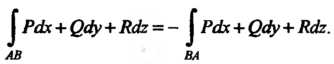
Криволинейные интегралы первого и второго рода связаны формулой
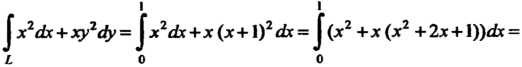
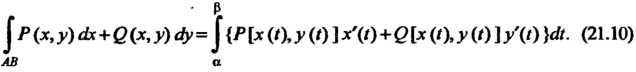

Где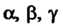 - углы между осями координат и направлением касательной к линии
- углы между осями координат и направлением касательной к линии
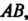 Отвечающим направлению интегрирования для интеграла в левой части.
Отвечающим направлению интегрирования для интеграла в левой части.
Вычисление криволинейного интеграла второго рода также сводится к вычислению определенного интеграла.
Если линия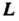 Задана параметрическими уравнениями
Задана параметрическими уравнениями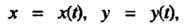
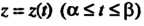 И значению а соответствует точка
И значению а соответствует точка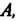 Значению
Значению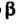 - точка
- точка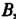 То
То
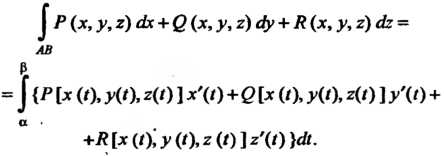 (21.9)
(21.9)
В частности, для кривой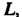 . лежащей в плоскости
. лежащей в плоскости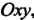 , получаем
, получаем
Если плоская кривая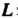 Задана уравнением
Задана уравнением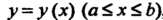 , то
, то
Пример 21.7. Вычислить криволинейный интеграл второго рода 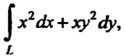 Где
Где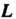 - отрезок прямой от точки
- отрезок прямой от точки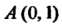 До точки
До точки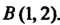
Уравнение прямой, проходящей через точки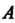 И
И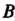 , имеет вид
, имеет вид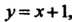 Поэто
Поэто
Му на отрезке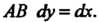 Подставляя в подынтегральную функцию вместо у его
Подставляя в подынтегральную функцию вместо у его
Выражение через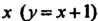 И замечая, что при перемещении от
И замечая, что при перемещении от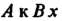 Меняется
Меняется
От 0 до 1, по формуле (21.11) получаем
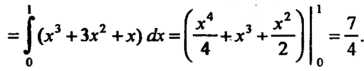
Пример 21.8. Вычислить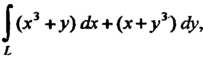 Где
Где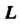 -ломаная
-ломаная
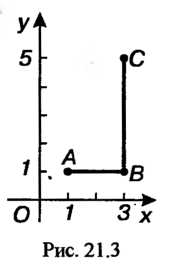
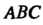 (рис. 21.3), причем
(рис. 21.3), причем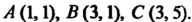
Так как контур интегрирования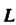 Состоит из двух отрезков
Состоит из двух отрезков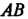 И
И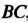 , то
, то
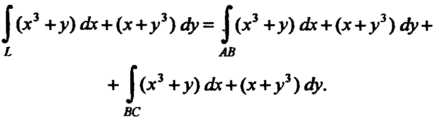
На отрезке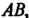 . уравнение которого
. уравнение которого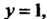 Имеем
Имеем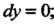 На
На
Отрезке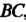 , уравнение которого
, уравнение которого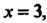 Имеем
Имеем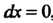 , поэтому
, поэтому
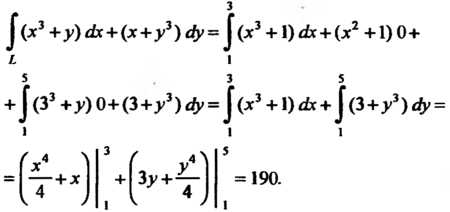
Пример 21.9. Вычислить криволинейный интеграл второго рода 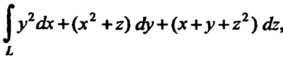 , где
, где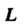 — отрезок прямой в пространстве от
— отрезок прямой в пространстве от
Точки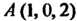 До точки
До точки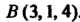
Составим сначала уравнения прямой, проходящей через точки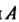 И
И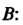

Из параметрических уравнений прямой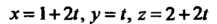 Получаем
Получаем
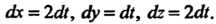
Из этих же уравнений видно, что при перемещении от точки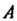 К точке
К точке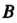 Параметр
Параметр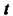 Меняется от 0 до 1, т. е. пределы интегрирования в формуле (21.10), которой воспользуемся, равны соответственно
Меняется от 0 до 1, т. е. пределы интегрирования в формуле (21.10), которой воспользуемся, равны соответственно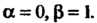 По формуле (21.10) находим
По формуле (21.10) находим
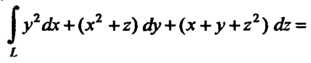
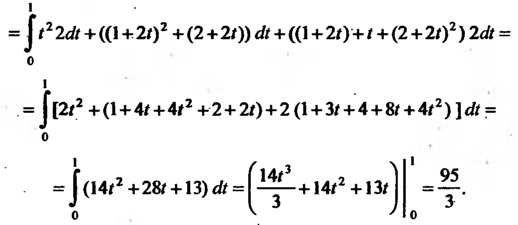
Пример 21.10. Вычислить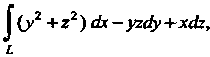 Где
Где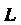 - дуга вин
- дуга вин
Товой линии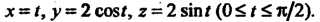
Поскольку То
То
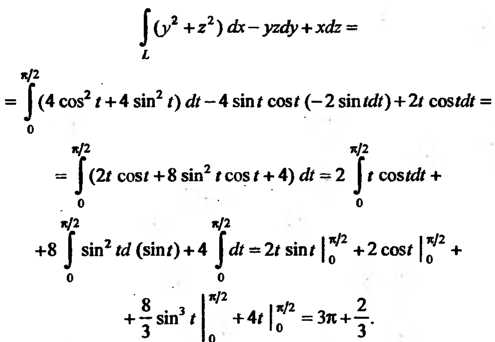
Замечание. Интеграл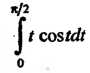 Вычислен с помощью метода
Вычислен с помощью метода
Интегрирования по частям:
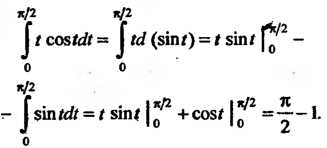
| < Предыдущая | Следующая > |
|---|