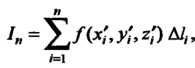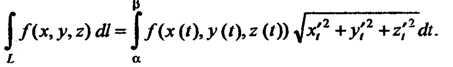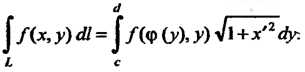21.1. Криволинейные интегралы первого рода

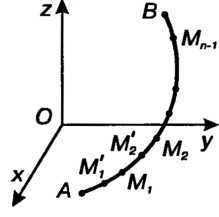
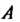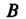Рассмотрим пространственную кусочно-гладкую кривую, ограниченную точкамиИ(рис. 21.1), и определенную на ней непрерывную функцию 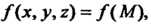Где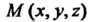- точка кривой. Дугу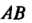Разобьем точками

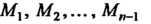На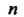Элементарных дуг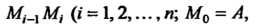

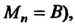Длины которых обозначим соответственно через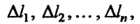А

Наибольшую из этих длин-через.На каждой из элементарных дуг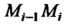Выберем произвольно

Одну точку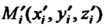И составим сумму

(21.1)

Называемую интегральной суммой для функции 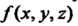По длине дуги кривой 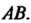Криволинейным интегралом первого родаили криволинейным интегралом по дуге кривой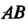От функции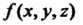Называется предел интеграль -  Рис - 21.1

Ной суммы (21.1) при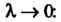

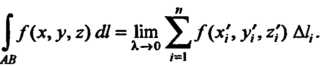
На кривой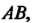Целиком лежащей на плоскости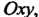Функция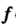От координаты 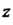не зависит, поэтому по определению имеем

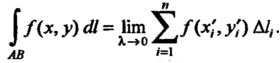
Если подынтегральную функцию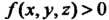Рассматривать как линейную

Плотность кривой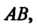То криволинейный интеграл первого рода представляет собой массу этой кривой.

Основные свойства криволинейного интеграла первого рода следующие.

1. Криволинейный интеграл первого рода не зависит от направления пути интегрирования: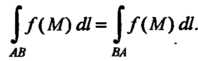

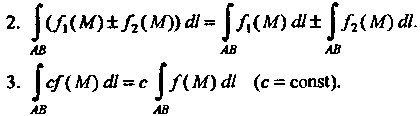
4. Если йуть интегрирования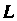Разбит на части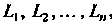, то

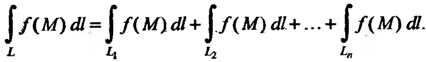
Вычисление 1фиволинейного интеграла первого рода сводится к вычислению определенного интеграла.

Если пространственная кривая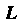Задана параметрическими уравнениями

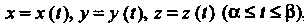, то

(21.2)

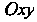Если криваяЛежит в плоскости, то

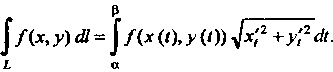(21.3)

В частности, для плоской кривой, заданной уравнени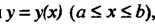емИмеем

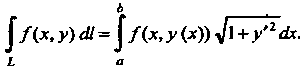(21.4)

Если плоская кривая задана уравнением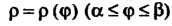В полярных

Координатах, то

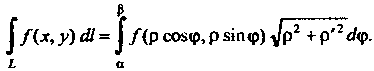(21.5)

Если кривая задана уравнением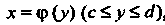, то криволинейный интеграл

Вычисляется по формуле

(21.6)

Пример 21.1. Вычислить криволинейный интеграл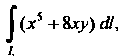, где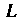

- дуга кривой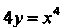Между точками, для которых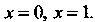

Поскольку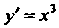,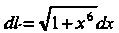И на дуге кривой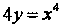Функция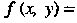

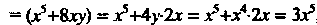, то по формуле (21.4) находим

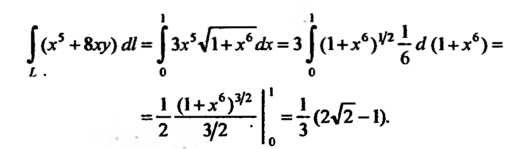
Пример 21.2. ВычислитьГде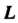- дуга кривой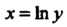

Между точками, для которых

Применяем формулу (2J.6). В данном случае

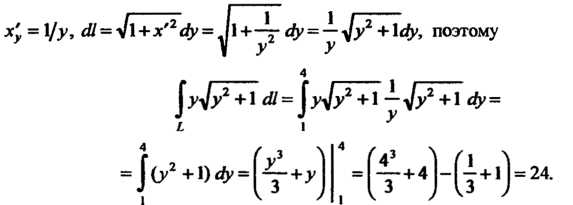
Пр имер 21.3. Вычислить криволинейный интеграл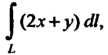Где-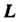

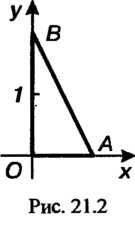
Контур треугольника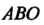(рис. 21.2) с вершинами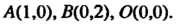

В соответствии со свойством 4) криволинейного интегра первого рода имеем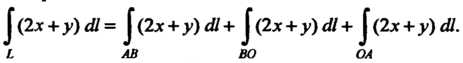

На отрезке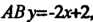Поэтому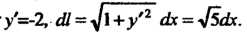

На отрезке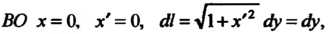На отрезке

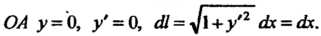Принимая во внимание свойство 1) криволинейного интеграла, используя формулы (21.4) и (21.6), получаем

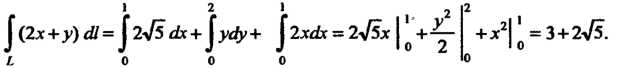
Пример 21.4. Вычислить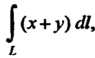Где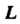- лепесток лемнискаты

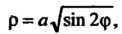Расположенный в первом координатном углу.

Линия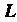Задана уравнением в полярных координатах, поэтому здесь целесообразно воспользоватьсяформулой (21.S).

Так как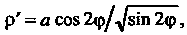То

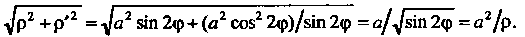
Заметив еще, что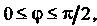Т. е.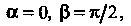По формуле (21.5) получим

Пример 21.5. Вычислить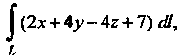Где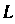- отрезок прямой

Между точками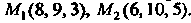

Составим сначала уравнения прямой, проходящей через точки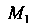И

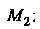
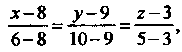Или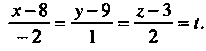

Таким образом, получаем параметрические уравнения прямой:

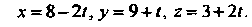
Точка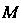Пробегает отрезок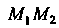, когда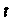Изменяется от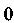До 1, т. е.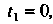

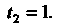Так как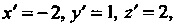То

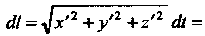
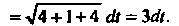
По формуле (21.2) находим

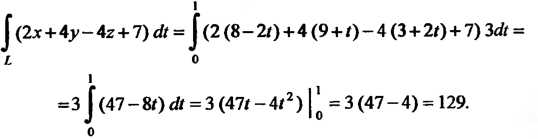
Пример 21.6. ВычислитьГде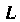-дуга винтовой линии

Отраниченной точками, для которых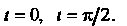 Применяем формулу (21.2). Поскольку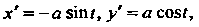

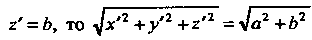И

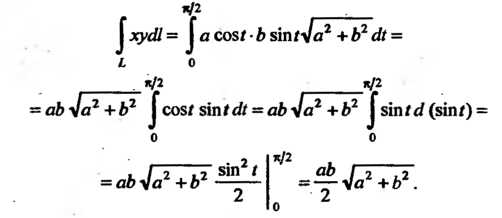
< Предыдущая		Следующая >