20.4. Приложения тройных интегралов

Объем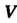Области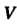Выражается формулой

(20.12)

В сферических координатах этот интеграл имеет вид

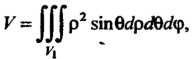
(20.13)

А в цилиндрических координатах

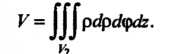
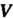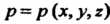Если тело занимает объемИ- плотность его в - точке

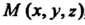, то масса тела равна

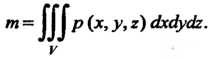(20.15)

Координаты центра тяжести тела вычисляются по формулам

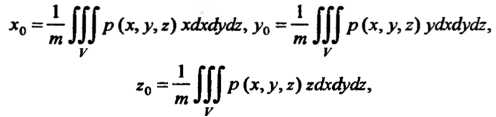(20.16)

Где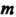— масса тела.

Моменты инерции тела относительно координатных плоскостей определяются интегралами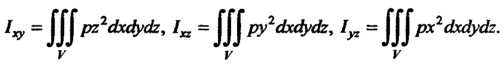

Момент инерции тела относительно оси Ои определяется интегралом

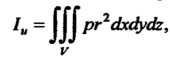
Где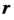— расстояние точки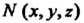Тела от осиВ частности, моменты инерции

Тела относительно координатных осей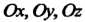Определяются формулами

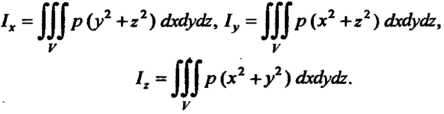(20.17)

Момент инерции тела относительно начала координат определяется формулой 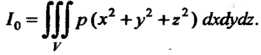 Очевидно, верны следующие соотношения: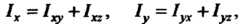

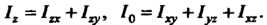
Ньютоновым потенциалом тела в точке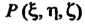Называется интеграл

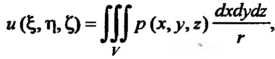(20.18)

Где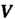— объем тела,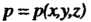- плотность тела,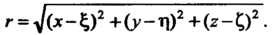

Материальная точка массы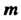Притягивается телом с силой, проекции которой 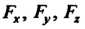На оси координат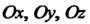Равны:

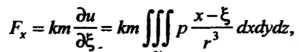
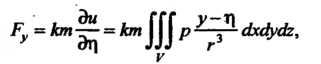
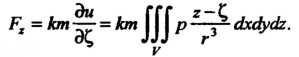
Пример 20.9. Найти объем тела, ограниченного поверхностями

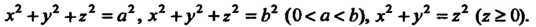
Данное тело ограничено сферами радиусов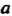И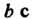Центрами в начале координат и конусом с вершиной в начале координат и осью, совпадающей с осью 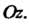Оно расположено над плоскостью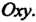Сечение этого тела плоскостьюИзображено на рис. 20.3.

Для вычисления объема тела перейдем к сферическим координатам по формулам (20.9). Уравнение сферы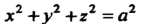Примет вид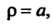Так как

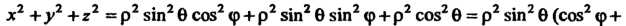
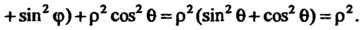Аналогично преобразуется уравнение второй сферы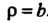. Уравнение конуса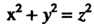Примет вид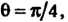Потому что

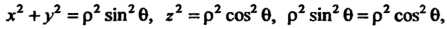Откуда

По формуле (20.13) находим

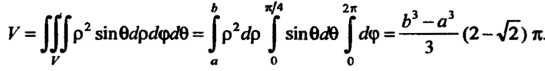
Пример 20.10. Вычислить объем тела, ограниченного поверхностями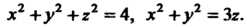

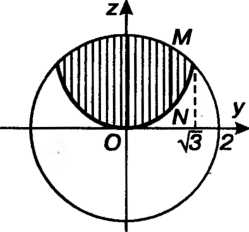
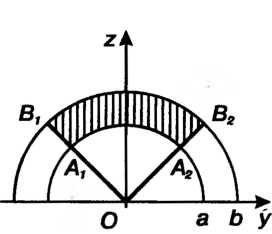
Рис. 20.3  Рис. 20.4

Данное тело ограничено сферой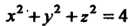И параболоидом вращения

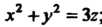; сечение тела плоскостью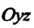Изображено на рис. 20.4. Для вычисления объема тела перейдем к цилиндрическим координатам по формулам (20.7). В цилиндрических координатах получаем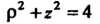(уравнение сферы),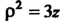

(уравнение параболоида). Отметим, что при постоянных значениях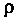И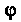Внутри тела z изменяется от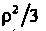(для точки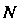Пересечения с поверхностью параболоида)

До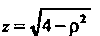(для точки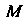Пересечения с верхней частью поверхности сферы).

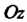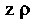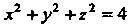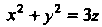При постоянномИзменяется от 0 (для точек, лежащих на оси) до наибольшего значения в точках линии пересечения данных поверхностей, так как с возрастаниемДля поверхности параболоида возрастает, а для шара убывает (что видно из уравнений поверхностей). Для линии пересечения поверхностей ИИмеем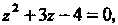Откуда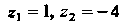

(второй корень дает мнимые значения для р). Следовательно, для точек линии пересечения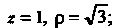Внутри тела р изменяется от 0 до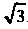. Заметив еще, что

Ф изменяется от 0 до 2тс, по формуле (20.14) получим

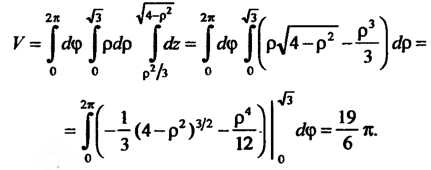
Пример 20.11. Вычислить объем тела, ограниченного эллипсоидом

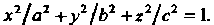
При наличии выражения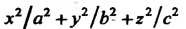В уравнении поверхности по

Лезен переход к обобщенным сферическим координатам по формулам (20.11). Якобиан в этом случае равен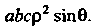

Уравнение данной поверхности в новых координатах примет вид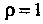(ибо

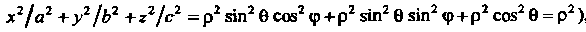, поэтому

Для данного тела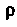Изменяется от 0 до 1. Заметив, чт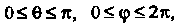оПо

Формуле (20.6) получим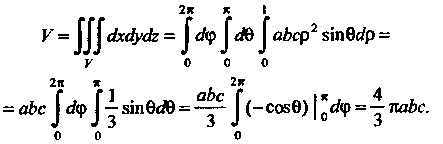

Итак,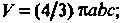В частном случае, при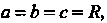Получаем объем ша

Ра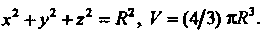

Замечание. Поскольку эллипсоидсимметричен относительно координатных плоскостей, то можно найти объем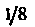Части данного тела. При вычислении интеграла нужно иметь в виду, что в этом случае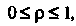

От предыдущих.

Пример 20.12. Найти массу шара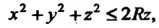Если плотность в

Каждой точке обратно пропорциональна расстоянию ее до начала координат.

Пусть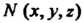- произвольная точка данного шара, тогда ее расстояниеДо

Начала координат выражается формулой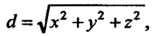Поэтому плотность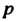В

Соответствиис условием задачи определяется формулой

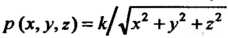, где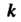- коэффициент пропорциональности. По

Формуле (20.15) имеем

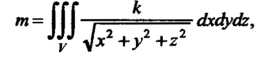
Где область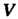Отраничена сферой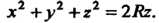Для вычисления данного

Интеграла перейдем к сферическим координатам по формулам (20.9). Подынтегральная функция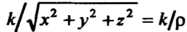, а уравнение сферы 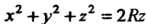примет вид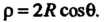

По формуле (20.10) находим

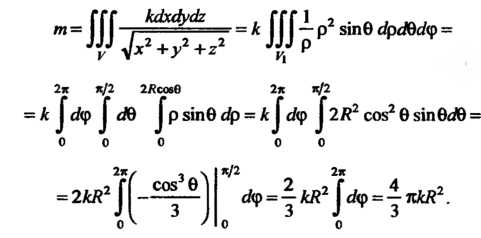
Пример 20.13. Найти центр тяжести шара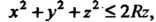 если плотность в каждой точке его обратно пропорциональна расстоянию до начала координат.

Воспользуемся формулами (20.16). Масса m была определена в предыдущей задаче (см. пример 20.12). Из соображений симметрии следует, что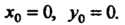Найдем

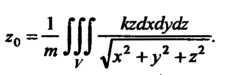
Замечание. Координаты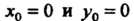Можно получить с помощью

Первых двух формул (20.16).

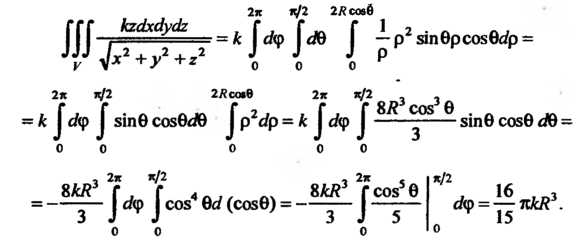
Следовательно,

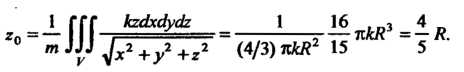
Пример 20.14. Вычислить момент инерции однородного куба относительно одного из его ребер.

Начало прямоугольной декартовой системы координат поместим в одной из вершин куба, а оси направим вдоль трех взаимно перпендикулярных ребер. Обозначим через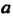Ребро куба и найдем его момент инерции относительно оси 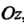воспользовавшись третьей из формул (20.17). Так как куб является однородным, то в указанных формулах можно положить:

Гпава 21

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

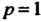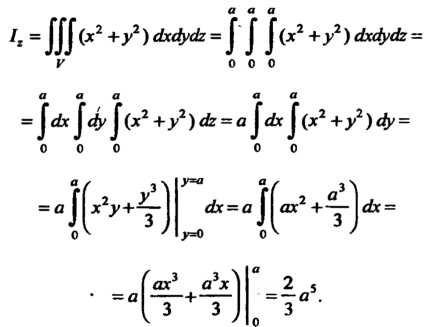
< Предыдущая		Следующая >