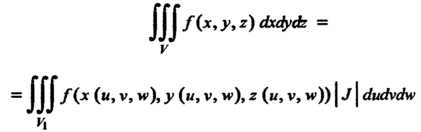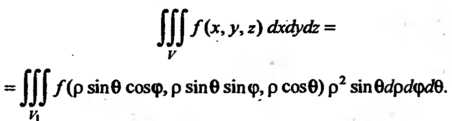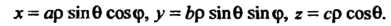20.3. Замена переменных в тройном интеграле
Если ограниченная замкнутая область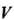 Пространства
Пространства Взаимно однозначно отображается на область
Взаимно однозначно отображается на область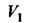 Пространства
Пространства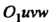 С помощью непрерывно дифференцируемых функций
С помощью непрерывно дифференцируемых функций
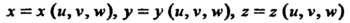 (20.4)
(20.4)
И якобиан

(20.5)
В области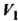 Не обращается в нуль, т. е.
Не обращается в нуль, т. е.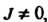 То замена переменных в тройном
То замена переменных в тройном
Интеграле осуществляется по формуле
В частности, при переходе от декартовых координат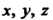 К цилиндрическим
К цилиндрическим
Координатам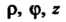 (см. п. 1.14), связанным с
(см. п. 1.14), связанным с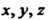 Формулами
Формулами
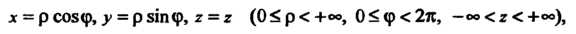
(20.7)
При переходе от декартовых координат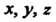 К сферическим
К сферическим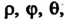 Связан
Связан
Ным с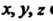 Соотношениями
Соотношениями
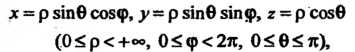 (20.9)
(20.9)
Якобиан преобразования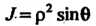 И формула (20.6) принимает вид
И формула (20.6) принимает вид
Пример 20.4. Вычислить тройной интеграл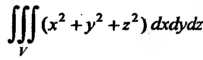 ,
,
Где область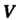 Есть шар
Есть шар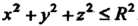
Перейдем к сферическим координатам по формулам (20.9). В области , являющейся образом области
, являющейся образом области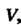 При преобразовании (20.9) переменные
При преобразовании (20.9) переменные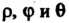 Меняются. в следующих пределах:
Меняются. в следующих пределах: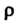 От
От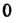 До
До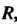
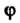 От
От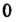 До
До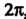 ,
,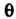 От
От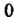 До
До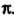 Так как подынтегральная функция
Так как подынтегральная функция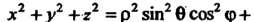
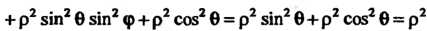 , а якобиан преобразования
, а якобиан преобразования
(20.9) равен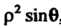 , то по формуле (20.10) получим
, то по формуле (20.10) получим
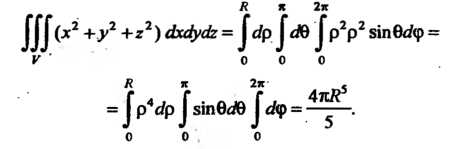
Пример 20.5. Вычислить тройной интеграл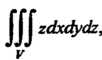 Где
Где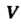 -
-
Область, ограниченная верхней частью конуса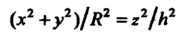 И плос
И плос
Костью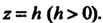
Введем цилиндрическиекоординаты по формулам (20.7). Уравнение конуса принимает вид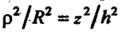 , или
, или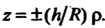
Новые переменные в области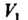 Изменяются в следующих пределах:
Изменяются в следующих пределах: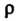 От
От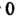 До
До 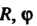 От
От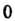 До
До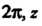 От
От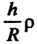 До
До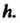
По формуле (20.8) получаем
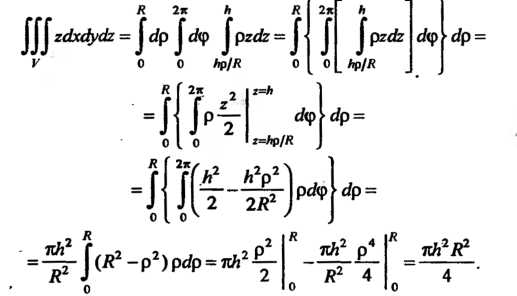
Пример 20.6. Вычислить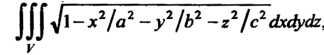 , где
, где
Область Ограничена эллипсоидом
Ограничена эллипсоидом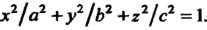
Введем так называемые обобщенные сферические координаты по формулам
Якобиан преобразования (20.11), определяемый формулой
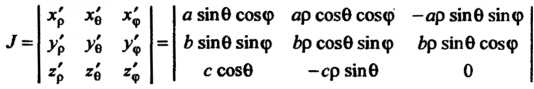
Равен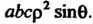 Подынтегральная функция по формулам (20.11) преобразуется к
Подынтегральная функция по формулам (20.11) преобразуется к
Виду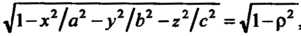 , а уравнение эллипсоида запишется так:
, а уравнение эллипсоида запишется так:
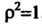 , или
, или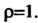
В области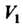 Переменные
Переменные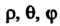 Изменяются в следующих пределах:
Изменяются в следующих пределах: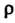 От
От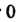 До
До
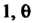 От
От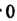 До
До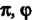 От
От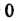 До
До По формуле (20.6) получаем
По формуле (20.6) получаем
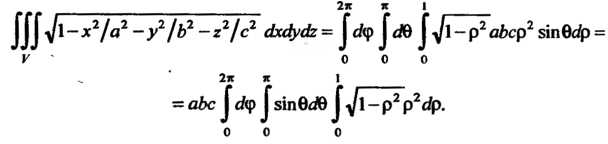
С помощью подстановки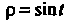 Находим первый интеграл:
Находим первый интеграл:
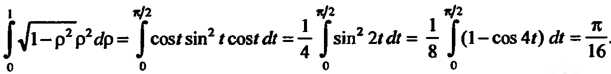
Далее,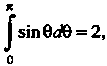 Поэтому
Поэтому

Пример 20.7. Вычислить тройной интеграл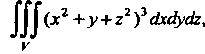
Где область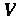 Ограничена цилиндром
Ограничена цилиндром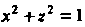 И плоскостями
И плоскостями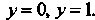
Перейдем к цилиндрическим координатам по формулам * = pcos<p,
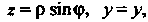 Тогда уравнение цилиндра
Тогда уравнение цилиндра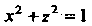 Примет вид
Примет вид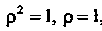
А подынтегральная функция запишется так:
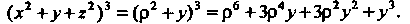
При таком переходе к цилиндрическим координатам замена переменных в тройном интеграле будет осуществляться по формуле
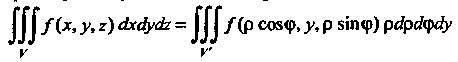
Следовательно,
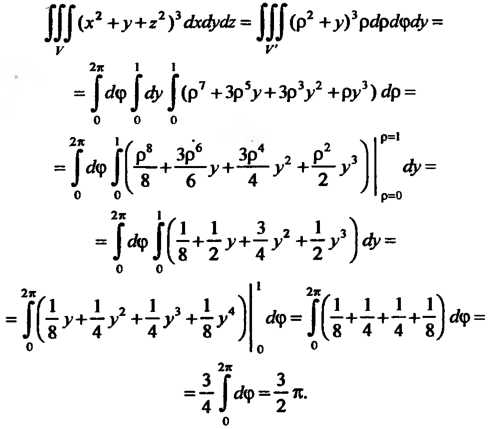
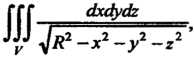
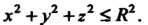
Грал где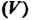 - шар
- шар
Данный интеграл является несобственным, так как подынтегральная функция не ограничена в рассматриваемой области (она обращается в бесконечность на границе области, т. е. на сфере _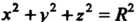 ).
).
Выражаем этот интеграл в сферических координатах. Так как в данном случае
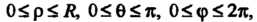 То по формуле (20.10) получаем
То по формуле (20.10) получаем
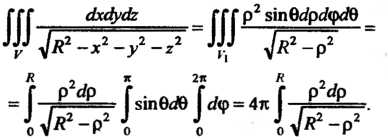

Последний интеграл (несобственный) вычислим с помощью подстановки
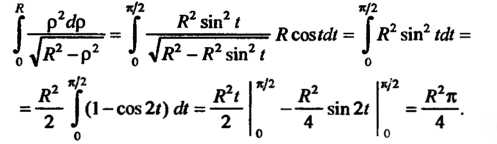
Итак,
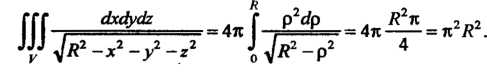
Следовательно, данный несобственный интеграл сходится и равен
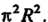
| < Предыдущая | Следующая > |
|---|