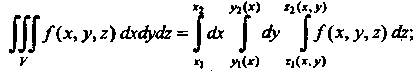20.2. Вычисление тройного интеграла в декартовых прямоугольных координатах

Если область интегрирования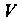Определяется неравенствами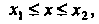

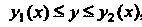
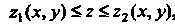, где

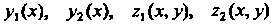
Непрерывные функции своих аргументов, то тройной интеграл вычисляется по формуле

(20.2)

Область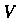Ограничена, сверху поверхностью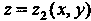, снизу - поверхностью

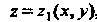, а с боков - цилиндрической поверхностью с образующими, параллельными оси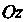(рис. 20.1), вырезающей на плоскости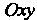Область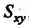, определенную неравенствами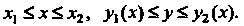

Отметим, что порядок интегрирования может быть изменен; тройной интеграл можно вычислить шестью различными способами (в формуле (20.2) первое интегрирование совершается по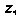Второе — по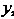, третье — по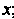; оставив первое интегрирование по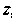, можно поменять местами второе и третье; далее, можно совершить первым интегрирование по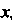, а так же по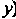I.

В частном случае, если функции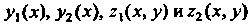Являются по

Стоянными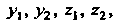Область интегрирования представляет собой црямо-

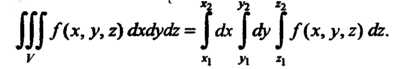
Пример 20.2. Вычислить тройной интеграл

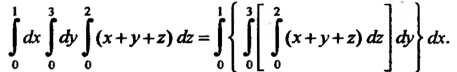
Эго интеграл вида (20.3). Пределы интегрирования в каждом из интегралов постоянные. Область интегрирования - прямой прямоугольный параллелепипед с измерениями 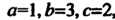, одна из вершин которого находится в начале координат. Вычисляем сначала внутренний интеграл, заключенный в квадратные скобки, считая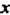И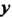Постоянными:

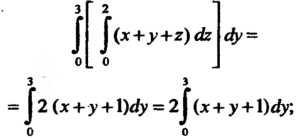
Находим этот интеграл, считая х постоянным:

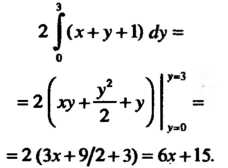
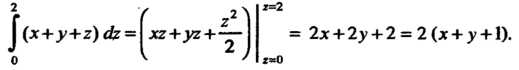
Второй интеграл, находящийся в фигурных скобках, принимает вид

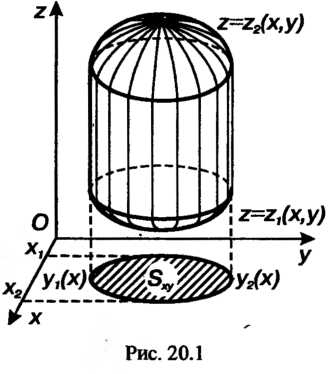
Вычислим, наконец, внешний интеграл:

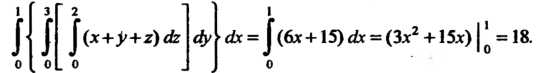
Замечание. Интегрирование можно производить и в другом порядке. В частности,

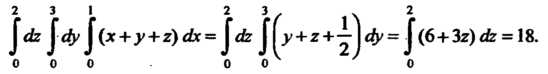
Рамида, ограниченная плоскостью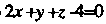И плоскостями координат (рис. 20.2, а).

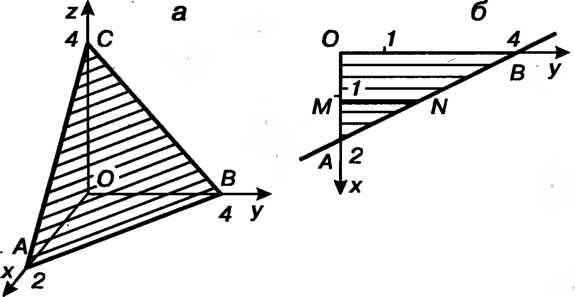
Рис. 20.2

Прежде всего расставим пределы интегрирования в данном тройном интеграле. Плоскость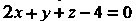Пересекает плоскость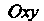По прямой

|, или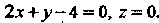В плоскости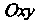Эта прямая, про

Ходящая через точкиИ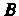(рис. 20.2, б), определяется уравнением 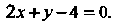Треугольник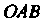И его внутренние точки являются областью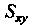Изменения переменных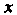И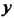(в эту область проектируется данная пирамида на плоскость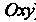). Очевидно,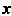Изменяется в промежутке [0,2], т. е.При фиксированном х

Из этого промежутка (абсцисса точки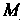)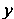Будет изменяться от 0 (ордината точки 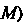До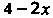(ордината точки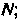; получена из уравнения прямой).

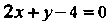При фиксированных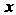И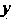Из области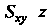Будет изменяться от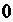До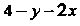

(получено из уравнения плоскости _).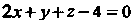

Таким образом,

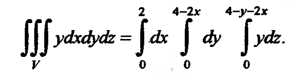
Поскольку

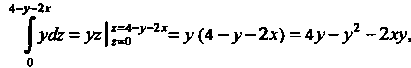
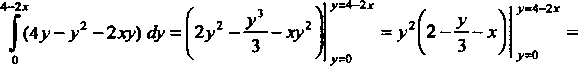
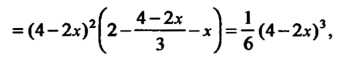
То

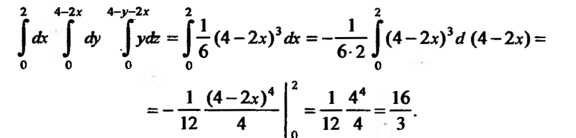
Замечание. Тот же результат можно получить, меняя порядок интегрирования. В частности, проецируя пирамиду на плоскость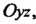Сводим данный тройной интеграл к следующему:

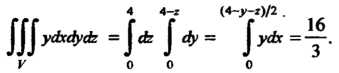
< Предыдущая		Следующая >