20.1. Понятие тройного интеграла. Оценка тройного интеграла

Рассмотрим замкнутую пространственную область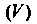И функцию 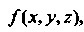определенную в этой области. Область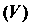Разобьем произвольным способом на 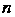элементарных областей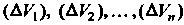С диаметрами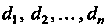И объ

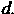
Емами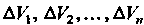. Наибольший из диаметров обозначим буквой... В каж

Дой элементарной области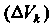Выберем произвольно одну точку

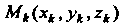И образуем произведение 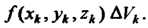Интегральной суммой для функции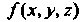По области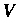Называется

Сумма вида

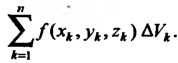
Тройным интегралом от функции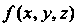По области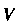Называется конечный

Предел ее интегральной суммы при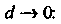

Если функция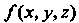Непрерывна в ограниченной области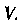, то указанный

Предел существует и конечен (он не зависит от способа разбиения области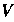На элементарные и от выбора точек).

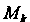В прямоугольных декартовых координатах тройной интеграл обычно запи-

Сывают в виде

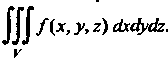
Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.

Если в области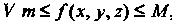, то

(20.1)

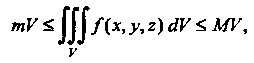
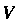
Где - объем области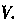Эти неравенства выражают оценку тройного интеграла.

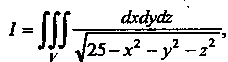
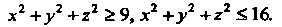
Где область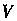Определена неравенствами

В данном случае область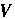Ограничена двумя сферами: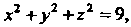

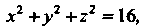Ее объем равен разности объемов двух шаров радиусов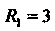И

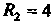С центрами в начале координат

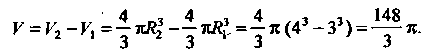
Подынтегральная функция принимает наибольшее значение на сфере 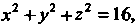Причем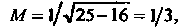А наименьшее - на сфере

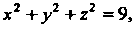
Следовательно, в соответствии с соотношениями (20.1) имеем

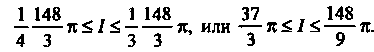
< Предыдущая		Следующая >