19.8. Несобственные двойные интегралы
Интегралы, распространенные на неограниченную область. Рассмотрим функцию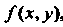
, определенную в неограниченной области
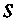. Предположим, что
Функция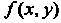
Интегрируема в любой конечной части
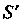Области
, т. е. суще
Ствует двойной интеграл
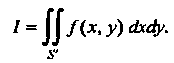(19.36)
Кривую
Отсекающую область
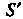, всеми ее точками станем удалять в бесконечность так, чтобы наименьшее расстояние
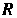От ее точек до начала координат неограниченно возрастало, а отсекаемая ею переменная область
Постепенно охватывала все точки области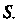
Несобственным интегралом от функции
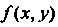В неограниченной области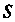
Называется предел (конечный или бесконечный) интеграла (19.36) при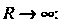
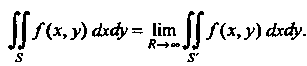(19.37)
В случае существования конечного предела интеграл (19.37) называется сходящимся, а в противном случае - расходящимся.
Функция, для которой интеграл (19.37) сходится, называется интегрируемой (в несобственном смысле) в области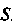
.
Приведение двойного интеграла к повторному. Путь функция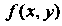
Задана в неограниченной области любого вида. Полагая ее равной нулю вне этой области, всегда можно свести дело к случаю неограниченной прямоугольной области - одному из прямоугольников: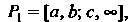
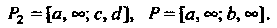
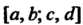
Если в каждом конечном прямоугольнике (при любых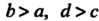
)
Существует в собственном смысле двойной интеграл от данной неотрицательной функции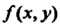
Н простой интеграл по
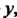То
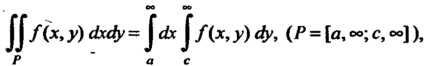(19.38)
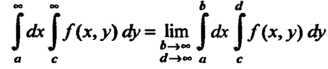(19.39)
В предположении, что повторный интеграл сходится.
Если функция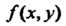
Меняет знак в бесконечной области
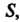То формула
(19.28) верна при дополнительном условии сходимости повторного интеграла от абсолютной величины данной функции:
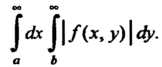(19.40)
Двойные интегралы от неограниченных функций. Пусть функция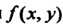
задана в ограниченной области
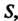Но оказывается неограниченной в окрестности некоторой точки
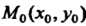, а в любой части области
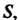Не содержащей этой точ
Ки, она является интегрируемой в собственном смысле.
Выделим особую точку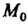
, окружив ее кривой
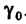. Если удалить из области
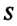окрестность, ограниченную кривой
, то получим область
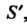Для которой существует двойной интеграл
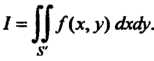(19.41)
Станем «стягивать» кривую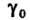
В точку
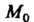Так, чтобы диаметр
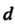Области, ограниченной
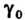, стремился к нулю.
Несобственным интегралом от неограниченной функции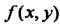
По области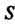
Называется предел интеграла (19.41) при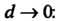
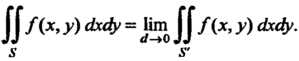(19.42)
Если указанный предел существует и конечен, то интеграл (19.42) называется сходящимся, в противном случае - расходящимся.
Аналогично определяется несобственный интеграл в случае, когда имеется несколько отдельных особых точек или указанные точки заполняют особую линию.
Замена переменных в несобственных двойных интегралах. В плоскост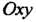и
и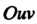
Рассмотрим ограниченные област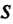и
И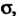
Связанные формулами преобразования:
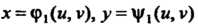Или обратными им:
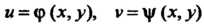С
345 соблюдением условий о которых шла речь в п. 19.3 (см. формулы (19.8) и (19.9)).
Пусть в области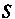
Задана функция
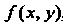, непрерывная всюду, за исключением ко
Нечного числа отдельных точек или даже кривых, где она обращается в бесконечность.
В этом случае выполняется равенство
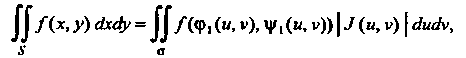(19.43)
Если сходится один из этих интегралов (сходимость другого следует отсюда).
Формула (19.43) верна и для случая неограниченных областей. Замена переменных наряду с переходом к повторному интегралу - удобное средство для установления сходимости несобственных двойных интегралов.
Пример 19.2S. Исследовать, сходится ли двойной интеграл
Где область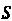
Определена неравенствами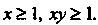
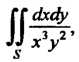
Данный двойной интеграл является несобственным, так как область интегрирования — бесконечная часть первого квадранта, ограниченная слева прямой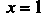
И снизу гиперболой
(рис. 19.23, а). Рассмотрим конечную часть области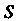
— область
Ограниченную линиями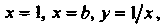
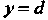(рис. 19.23, б, область
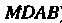). В области
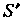Двойной интеграл существует в собственном смысле (при любых
):
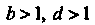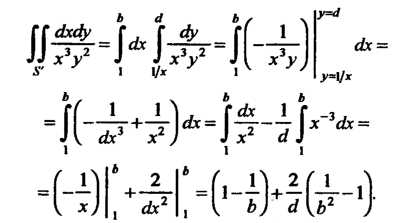
Поскольку подынтегральная функция положительна во всей области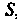
, то в соответствии с формулами (19.38) и (19.39) имеем
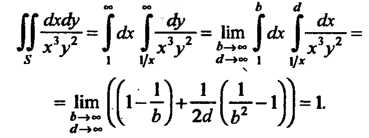
Следовательно, данный несобственный двойной интеграл сходится и равен единице.
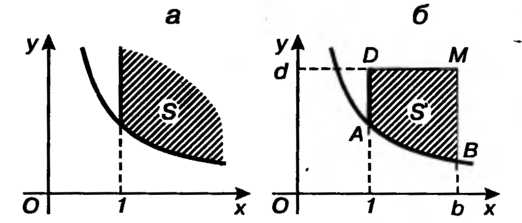
Рис. 19.23
Пример 19.26. Исследовать, сходится ли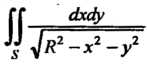
, где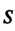
-
Круг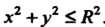
Данный двойной интеграл является несобственным, так как подынтегральная функция не ограничена в данной области (на границе области, т. е. на окружности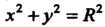 
, она обращается в бесконечность). Для решения вопроса о сходимости интеграла перейдем к полярным координатам по формулам
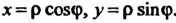. Имеем
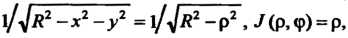Пределы
Интегрирования: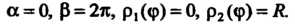
Формула (19.43) в данном случае принимает вид
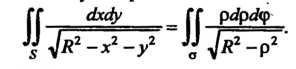
Так как
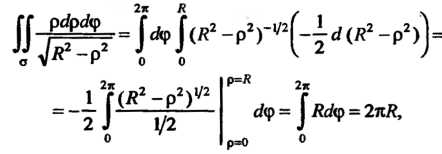
То
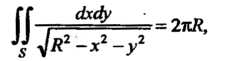
Т. е. двойной несобственный интеграл сходится и равен 2nR.
Пример 19.27. Установить условия сходимости интеграла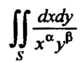
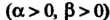, где область
Определена неравенствами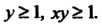
Областью интегрирования является бесконечная часть первого квадранта, ограниченная прямой
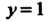И гиперболой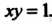
Рассмотрим конечную часть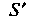
Данной области, ограниченную линиями
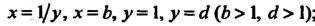I двойной интеграл по области
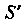Существует. Действительно,
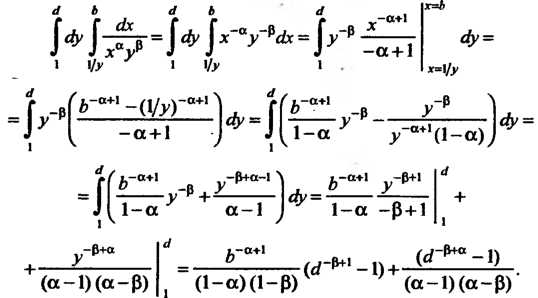
Предел этого интеграла при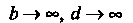
Существует, когда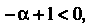
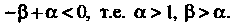При выполнении этих условий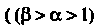
Пример 19.28. Доказать, что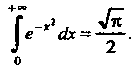
Рассмотрим квадрат этого интеграла, для чего воспользуемся формулами (17.3), (19.7) и перейдем к полярным координатам при вычислении полученного двойного интеграла:
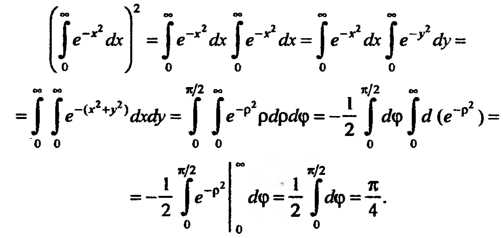
Следовательно,
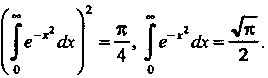
| < Предыдущая | Следующая > |
|---|
