19.7. Приложения двойных интегралов в механике

Масса и статические моменты пластинки. Если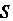- область плоскости 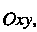занятая пластинкой, а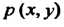- поверхностная плотность в точке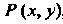,¦ то

Масса пластинкиВыражается формулой

(19.26)

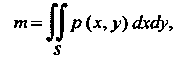
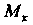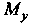А статические моментыИОтносительно осе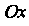йИОпределяются двойными интегралами

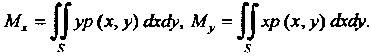(19.27)

Если пластинка однородна, то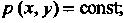Эту постоянную часто полагают

Равной 1.

Координаты центра тяжести пластинки. Если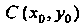— центр тяжести

Пластинки, то

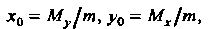(19.28)

Где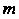- масса пластинки,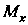,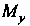- ее статические моменты относительно

Осей координат, определяемые соответственно формулами (19.26) и (19.27).

В случае однородной пластинки формулы (19.28) с учетом формул (19.26),

(19.27) принимают вид

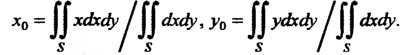(19.29)

(В формулах (19.29) знаменатель дроби - площадь пластинки, центр тяжести которой отыскивается).

Момент инерцнн пластинки. Моменты инерции пластинки относительно осе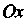йИ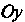Соответственно определяются формулами:

Момент инерции пластинки относительно начала координат

Полагая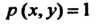В формулах (19.30) и (19.31), получаем геометрические

Моменты инерции плоской фигуры.

Координаты центр» тяжести теля. Если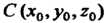- центр тяжести од

Нородного вертикального цилиндрического тела, имеющего своим основанием область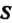Иа плоскости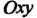И ограниченного поверхностью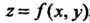, то

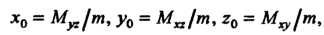(19.32)

Где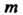- масса тела, а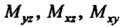- статические моменты тела относительно

Плоскостей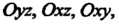Определяемые формулами:

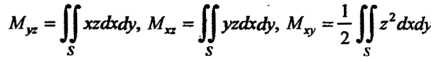(19.33)

Моменты инерцнн цилиндрического теля. Моменты инерции цилиндрического тела, ограниченного поверхностью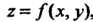, ее проекцией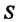На плоскость

И проецирующим цилиндром с образующими, параллельными оси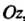, относительно этой оси и относительно плоскостейВыражаются формулами

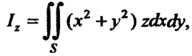(19.34)

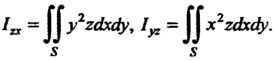(19.35)

При вычислении двойных интегралов в формулах (19.26) - (19.35) во многих случаях целесообразно перейти к полярным координатам.

Пример 19.21. Найти массу круглой пластинки радиуса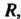Если поверхностная плотность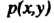Материала пластинки в каждой точке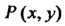Пропорциональна расстоянию Точки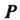От центра круга.

Начало прямоугольной декартовой системы координат поместим в центре круга, тогда координаты любой его точки удовлетворяют соотношению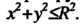 Расстояние от точки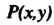До начала координат определяется формулой

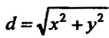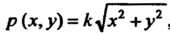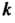, поэтому в соответствии с условием будем иметь ,где- коэффициент пропорциональности.

По формуле (19.26) имеем

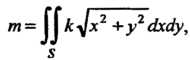
- круг

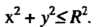
Где

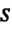
Переходя к полярным координатам, находим

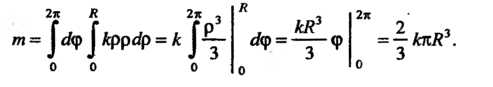
Пример 19.22. Найти статические моменты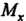И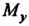Фигуры, лежащей в первой четверти, ограниченной эллипсом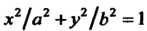И координатными осями, если в каждой точке фигуры плотность пропорциональна произведению координат этой точки.

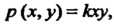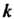По условию имеемГде- коэффициент пропорциональности,

Поэтому формулы (19.27) для данного случая примут вид

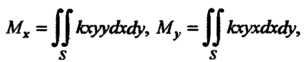
Где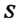- область, ограниченная дугой эллипса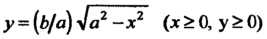И

Координатными осями.

Найдем сначала статический момент данной фигуры относительно оси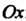

Так как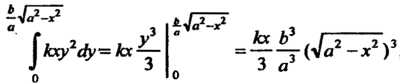, то

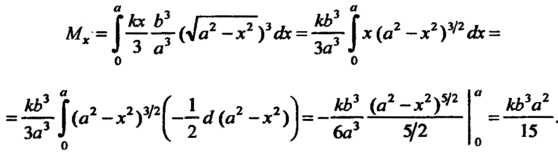
Аналогично находим статический момент фигуры относительно оси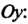

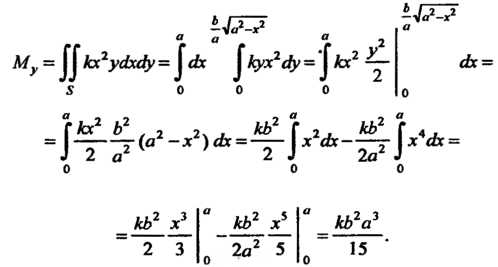
Пример 19.23. Найти центр тяжести фигуры, указанной в примере 19.22. Координаты центра тяжести плоской фигуры определяются формулами

(19.28). Статические моменты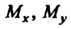Найдены в примере 19.22, осталось вычис

Лить массу данной фигуры.

По формуле (19.26) находим

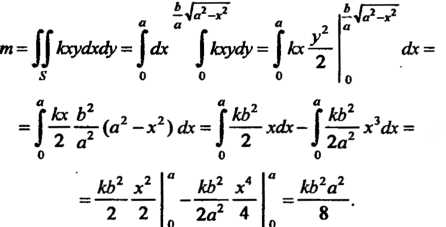
Так как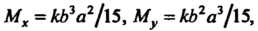То по формулам (19.28) имеем

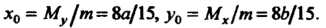
Пример19.24. Найти центр тяжести однородной фигуры, ограниченной параболой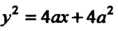И прямой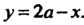

Воспользуемся формулами (19.29), для чего вычислим предварительно входящие в них двойные интегралы.

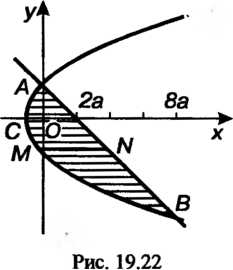
Найдем сначала интеграл, стоящий в знаменателе; он выражает площадь данной фигуры. Решая совместно уравнения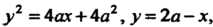

Находим точки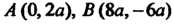Пересечения

Параболы и прямой (рис. 19.22).

В области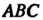При фиксированном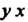Меняется от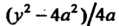(абсцисса точки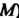J до

(абсцисса точки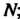; выражения для абсцисс точек

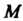И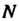Получены из уравнений линий решением относительно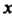), а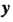Меняется от 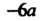(ордината точки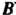) до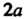(ордината точки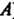). Следовательно,

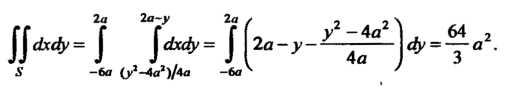
Вычисляем интегралы, стоящие в числителях формул (19.29):

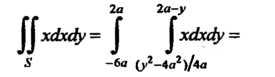
По формулам (19.29) находим координаты центра тяжести:

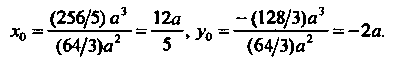
< Предыдущая		Следующая >