19.6. Вычисление площадей поверхностей
Случай явного задания поверхности. Площадь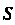 Гладкой поверхности
Гладкой поверхности 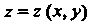 Выражается формулой
Выражается формулой
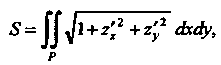 (19.19)
(19.19)
Где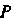 - проекция данной поверхности на плоскость
- проекция данной поверхности на плоскость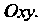
Если поверхность имеет уравнение вида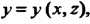 То
То
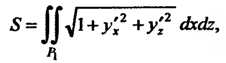 (19.20)
(19.20)
Где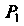 — проекция поверхности на ось
— проекция поверхности на ось
Если поверхность задана уравнением,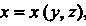 , то
, то
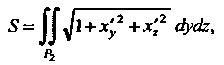 (19.21)
(19.21)
Где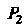 — проекция поверхности на ось
— проекция поверхности на ось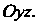
Случай неявного задания поверхности. Площадь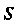 Поверхности, заданной уравнением
Поверхности, заданной уравнением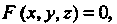 Выражается интегралом
Выражается интегралом
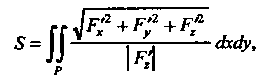 (19.22)
(19.22)
Где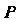 - проекция поверхности на плоскость
- проекция поверхности на плоскость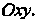
Случай параметрического задания поверхности. Если поверхность задана параметрическими уравнениями
Где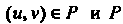 - ограниченная замкнутая квадрируемая область, в которой
- ограниченная замкнутая квадрируемая область, в которой
Функции х, у, z непрерывно дифференцируемы, то
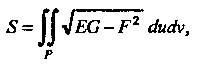
(19.24)
Где
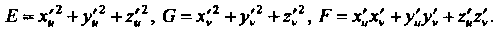 (19.25)
(19.25)
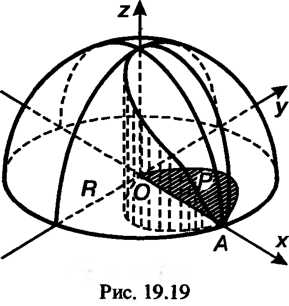
Пример 19.17. Найти площадь части поверхности цилиндра 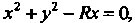 Заключенной внутри сферы
Заключенной внутри сферы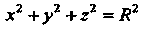 (боковая поверх
(боковая поверх
Ность «тела Вивиани», рис. 19.19).
Применим формулу (19.20). Поскольку плоскостью Цилиндр разделяется на две равные части, то можно вычислить половину искомой площади поверхности. Вычислим площадь той части поверхности, уравнение которой
Цилиндр разделяется на две равные части, то можно вычислить половину искомой площади поверхности. Вычислим площадь той части поверхности, уравнение которой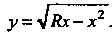 Для определения области интегрирования
Для определения области интегрирования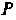 следует спроецировать на плоскость
следует спроецировать на плоскость линию пересечения поверхностей, уравнение которой находится исключением
линию пересечения поверхностей, уравнение которой находится исключением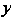 Из данных уравнений. Вычитая одно уравнение из другого, получаем
Из данных уравнений. Вычитая одно уравнение из другого, получаем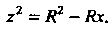 Это
Это
Так как
Уравнение параболы, лежащей в плоскости 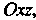 С вершиной на оси
С вершиной на оси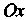 На расстоянии
На расстоянии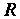 от начала координат и пересекающей ось
от начала координат и пересекающей ось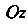 в точках
в точках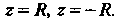 Дуга указанной
Дуга указанной
Параболывместе с соответствующим отрезком оси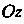 Составляют границу области.
Составляют границу области.
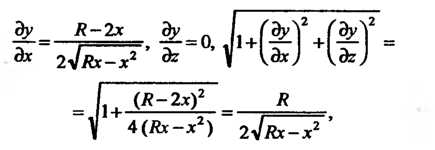
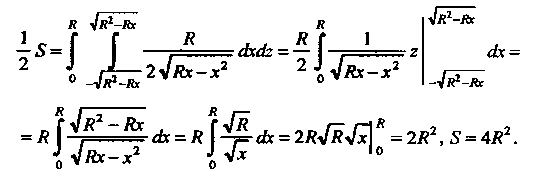
Пример 19.18. Вычислить площадь поверхности конуса 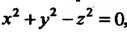 , заключенной внутри цилиндра
, заключенной внутри цилиндра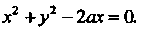 Цилиндр отсекает на поверхности конуса две части, симметричные относительно плоскости
Цилиндр отсекает на поверхности конуса две части, симметричные относительно плоскости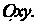 На рис. 19.20 изображена только верхняя часть
На рис. 19.20 изображена только верхняя часть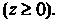 Вычислим пло
Вычислим пло
Ишь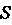 Этой части, проекция которой на плоскость
Этой части, проекция которой на плоскость Есть круг
Есть круг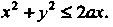
Так как для рассматриваемой части конуса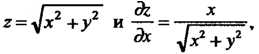
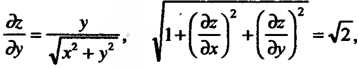
То по формуле (19.19)
Получаем

Где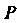 - окружность
- окружность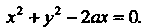 Переходя к полярным координатам, находим
Переходя к полярным координатам, находим
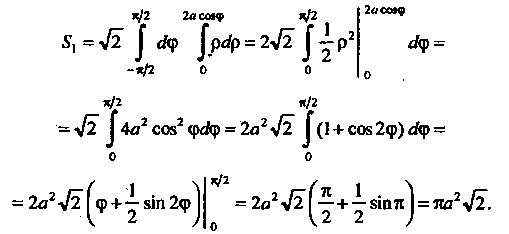
Следовательно, вся искомая площадь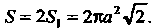
Пример 19.19. Найти площадь поверхности, вырезанной цилиндром 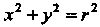 Из сферы
Из сферы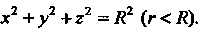
Цилиндр вырезает из сферы две части, верхняя из них изображена на рис. 19.21. Вычислим площадь Поверхности этой сферы. Для верхней полусферы
Поверхности этой сферы. Для верхней полусферы

Следовательно,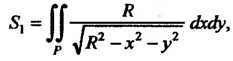
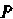 - круг
- круг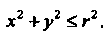
Переходя к полярным координатам, находим 338
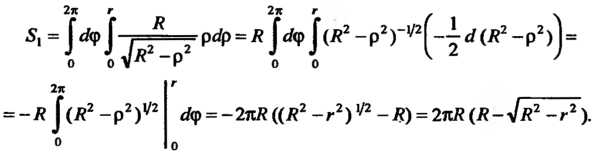
Итак,
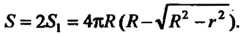
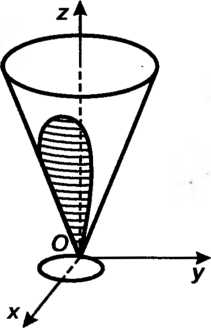
Рис. 19.20
Пример 19.20. Вычислить площадь частей сферы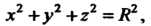 вырезанных из нее цилиндром
вырезанных из нее цилиндром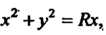 Воспользовавшись параметрическими
Воспользовавшись параметрическими
Уравнениями сферической поверхности:
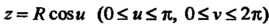
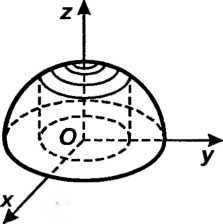
Рис. 19.21
Здесь вдет речь о вычислении площади верхнего и нижнего оснований «тела Вивиани» (см. рис. 19.19). Воспользуемся формулой (19.24), для чего предварительно найдем коэффициенты Так как
Так как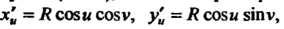
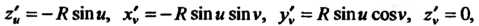 То по формулам (19.25)
То по формулам (19.25)
Находим Следовательно,
Следовательно,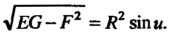
Ограничимся рассмотрением четверти изучаемой поверхности, лежащей в первом октанте. Для точек «кривой Вивиани», т. е. кривой пересечения сферы и цилиндра (в пределах первого октанта),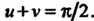 Действительно подставляя выражения
Действительно подставляя выражения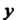 И
И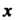 Через
Через И
И В уравнение цилиндра
В уравнение цилиндра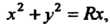 Получаем
Получаем 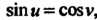 И поскольку для рассматриваемых точек, очевидно,
И поскольку для рассматриваемых точек, очевидно, 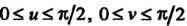 , то отсюда следует, что
, то отсюда следует, что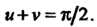
Установив на основании сказанного пределы изменения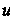 И
И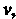 По формуле (19.24) получим
По формуле (19.24) получим
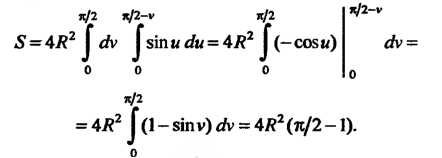
| < Предыдущая | Следующая > |
|---|