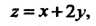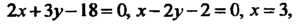19.5. Вычисление объемов тел

Объем цилиндроида, ограниченного сверху непрерывной поверхностью 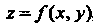, снизу плоскостью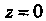И с боков прямой цилиндрической поверхностью, вырезающей из плоскости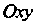Область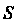(см. рис. 19.2), вычисляется по формуле

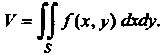(19.18)

Пример 19.12.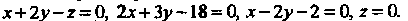Вычислить объем тела, ограниченного плоскостями Данное тело ограничено сверху плоскостью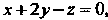Или

О)

С боков плоскостями

(2)

Параллельными оси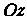(уравнения не содержат координаты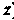>, и снизу - плоскостью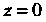(плоскостью).

332

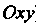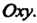
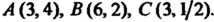
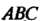
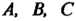
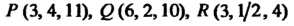
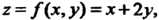
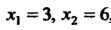
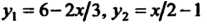
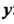
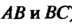
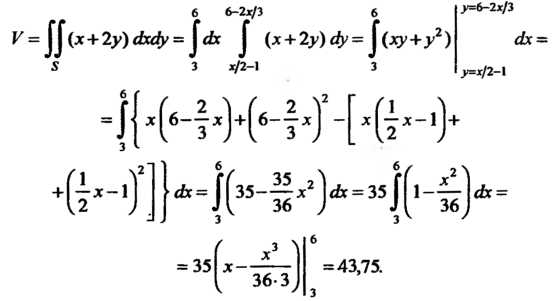
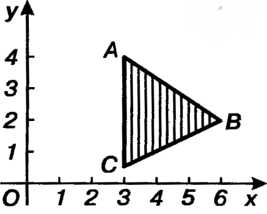
В плоскости Оху (2 = 0) уравнения (2) являются уравнениями прямых, по которым плоскости (2) пересекают плоскость Оху. Решая каждые два из них, находим три точки пересечения: А (3,4), В (6,2), С (3,1/2). Следовательно, плоскости

(2) вырезают в плоскости Оху область 5, которая является треугольником АВС (рис. 19.14). На плоскости (1) точкам А, В, С будут соответствовать точки Р (3,4,11), ^ (6,2,10), К (3,1/2,4) - вершины данного тела.

Так как в данном случае г = /(х, у) = л + 2у, пределы интегрирования по х: л,=3, х2=6, пределы интегрирования по у: у1-6-2х/3,у2=х/2~1 (получено из уравнений прямых АВ и ВС), то по формуле (19.18) находим

Б 6-2х/3  6  >=6-2*/3

V = ^^^x+2у)<Шу = ^(^x | (х + 2у)ф = ^(xу+у2)

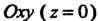
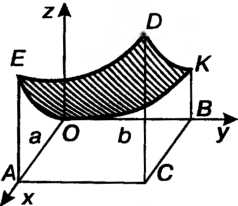
Пример 19.13. Вычислить объем тела, ограниченного поверхностью х2+у2— 2 = 0, координатными плоскостями и плоскостями х = а, у = Ь, (а > 0, Ь > 0).

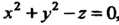
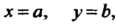
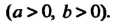
Данная поверхность является параболоидом вращения с вершиной в начале координат и осью, совпадающей с осью Ог. Тело, ограниченное этой поверхностью и указанными плоскостями, изображено на рис. 19.15. Область 5, вырезаемая плоскостями х = 0, х = а, у = 0, у = Ь, является прямоугольником ОАСВ.

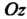
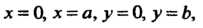
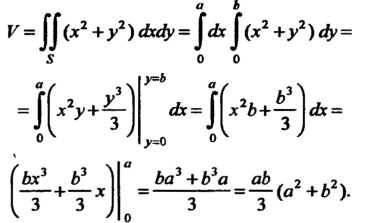
Пример 19.14. Найти объем тела, ограниченного поверхностью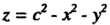И

Плоскостями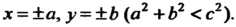

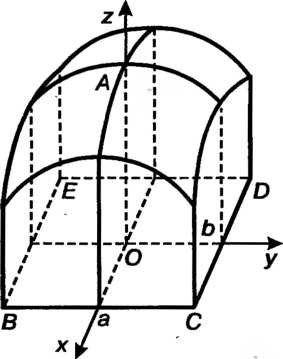
Поверхность, ограничивающая цилиндрическое тело сверху, является параболоидом вращения с вершиной в точке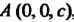, область интегрирования - прямоугольник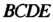Со сторо-

Рис. 19.16

Нами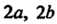И цешром в начале координат (рис. 19.16).

Объем тела

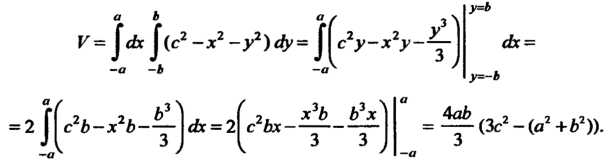
Замечание. Исходя из соображений симметрии, данный объем можно вычислить по формуле

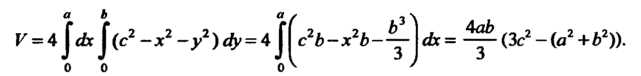
Пример 19.15. Вычислить объем тела, ограниченного поверхностью 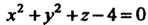И плоскостью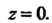

Разрешая первое уравнение относительно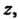Получаем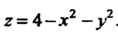. Это

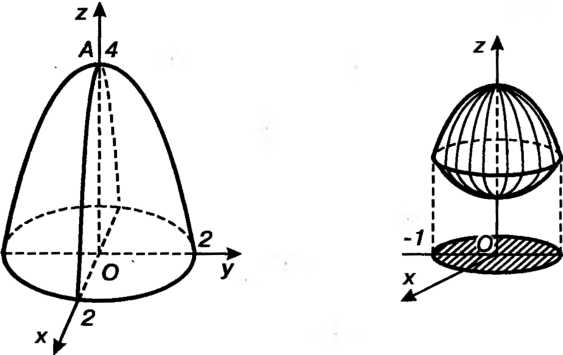
Уравнение определяет параболоид вращения с вершиной в точке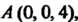 являющейся высшей точкой поверхности (рис. 19.17). Параболоид 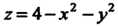И плоскость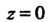Пересекаются по окружности, уравнение

Которой в плоскости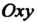Имеет вид 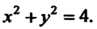334

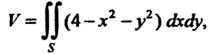
Где область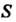Ограничена окружностью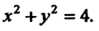

Чтобы вычислить интеграл, перейдем к полярным координатам по форму-

Лам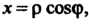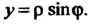Так как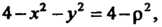

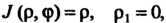
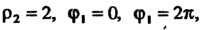То

¦>

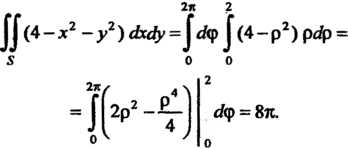
У

Рис. 19.17

1

Рис. 19.18

Пример 19.16. Вычислить объем тела, ограниченного поверхностями

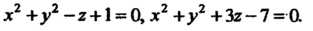
Данное тело ограничено двумя параболоидами (рис. 19.18). Линии пересечения параболоидов определяются системой уравнений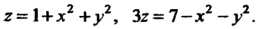

Исключая из этих уравнений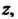Получаем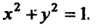Из первого уравнения при

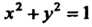Имеем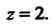Итак, линией пересечения является окружность

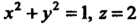(пересечение прямого кругового цилиндра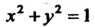И плос

Кости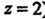). Проекция этой линии на плоскость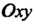Также является окружностью

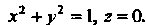
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием и ограниченных сверху и снизу соответственно поверхностям: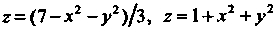, т. е.

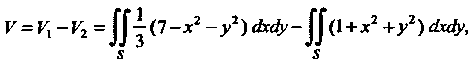
Где область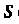Есть круг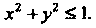

Переходя к полярным координатам, находим

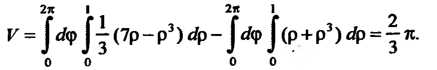
< Предыдущая		Следующая >