19.4. Вычисление площадей плоских областей
Площадь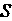 Плоской области-
Плоской области-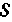 Выражается формулой
Выражается формулой
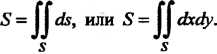
(19.15)
В криволинейных координатах этот интеграл имеет вид
(19.16)
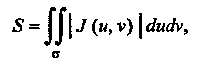
В полярных координатах
(19.17)
Пример 19.8. Вычислить площадь области, ограниченной линиями
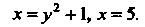
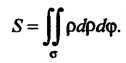
Данная область ограничена параболой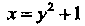 И прямой
И прямой (рис. 19.12).
(рис. 19.12).
Решая систему уравнений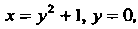 Находим точку
Находим точку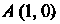 Пересечения
Пересечения
Параболы с осью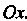 Из системы уравнений
Из системы уравнений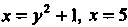 Находим две точки
Находим две точки
Пересечения параболы с прямой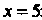
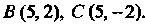 Область
Область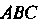 Можно
Можно
Рассматривать как область первого вида и как область второго вида.
Применяя формулу (19.15) и рассматривая область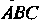 Как область первого вида, находим
Как область первого вида, находим
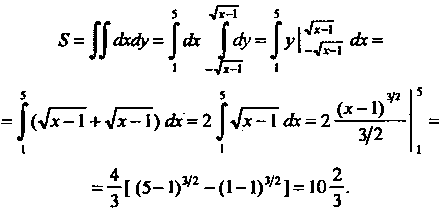
Замечание. Рассматривая область Как область второго вида, получаем
Как область второго вида, получаем
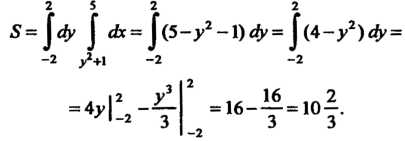
Пример 19.9. Вычислить площадь области, ограниченной линиями 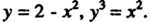 По формуле (19.15) получаем
По формуле (19.15) получаем
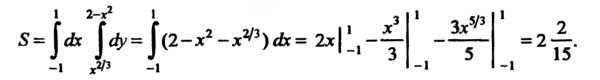
Пример 19.10. Вычислить площадь фигуры, ограниченной лемнискатой Бернулли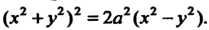
В силу симметрии кривой относительно осей координат достаточно вычислить площадь одной четверти данной фигуры. Переходим к полярным координатам, полагая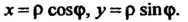 Полярное уравнение лемнискаты имеет вид
Полярное уравнение лемнискаты имеет вид
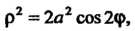 Или
Или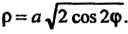 Для части фигуры расположенной в первом
Для части фигуры расположенной в первом
Координатном углу, имеем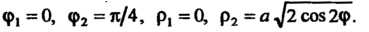
Обозначая площадь этой фшуры через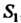 , по формуле (19.17) получаем:
, по формуле (19.17) получаем:
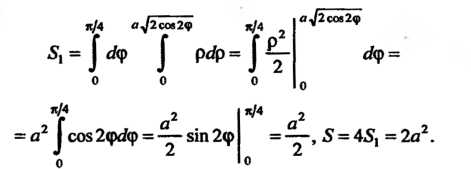
Пример 19.11. Найти площадь фигуры, ограниченной линиями:
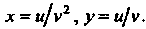
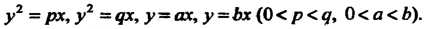
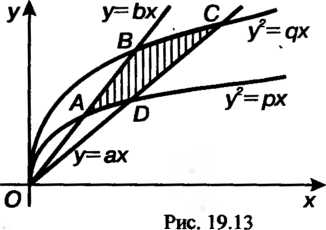
Фигура представляет собой криволинейный четырехугольник, ограниченный двумя параболами и двумя прямыми, проходящими через начало координат (рис. 19.13). Введем новые криволинейные координаты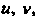 Связанные с координатами
Связанные с координатами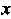 И
И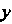 Формулами
Формулами
- Эта замена переменных подсказана видом области интегрирования (в качестве новых переменных взяты параметры, входящие в уравнения линий, ограничивающих данную фигуру). Из уравнений (1) выражаем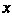 И
И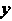 Через
Через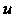 И
И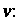
Находим якобиан преобразования (2):
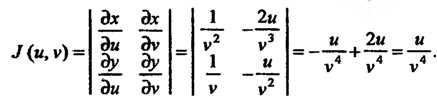
По формуле (19.16) получаем
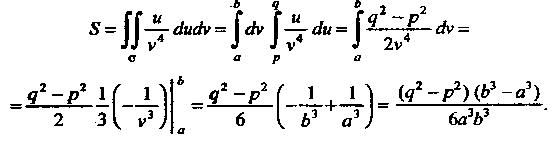
| < Предыдущая | Следующая > |
|---|