19.3. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах
Криволинейные координаты ия плоскости. Рассмотрим непрерывно дифференцируемые функции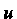 И
И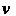 Прямоугольных декартовых координат
Прямоугольных декартовых координат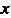 И
И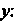
Предположим, что уравнения (19.8) однозначно разрешимы относительно х и у:
 (19.9)
(19.9)
Где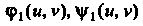 - непрерывно дифференцируемые функции
- непрерывно дифференцируемые функции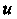 И
И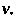
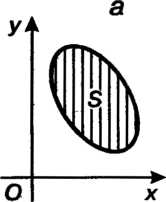
Придавая поочередно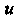 И
И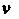 Различные (возможные для них) постоянные значения, получаем два семейства линий на плоскости (рис. 19.8, а); эти линии называют координатными линиями. Положение точки
Различные (возможные для них) постоянные значения, получаем два семейства линий на плоскости (рис. 19.8, а); эти линии называют координатными линиями. Положение точки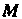 На плоскости определяется парой чисел
На плоскости определяется парой чисел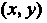 Или парой чисел
Или парой чисел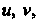 Где
Где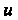 И
И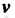 Выражены формулами (19.8).
Выражены формулами (19.8).
Числа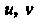 Называются криволинейными координатами точки
Называются криволинейными координатами точки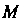 На плоскости. Примером криволинейных координат являются полярные координаты, в этом случае
На плоскости. Примером криволинейных координат являются полярные координаты, в этом случае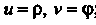 ; координатные линии - концентрические окружности и полу
; координатные линии - концентрические окружности и полу
Прямые, исходящие из начала координат (рис. 19.6, б). Прямоугольные координаты - также частный случай криволинейных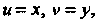 Координатные линии - прямые, параллельные осям координат (рис. 19.8, в).
Координатные линии - прямые, параллельные осям координат (рис. 19.8, в).
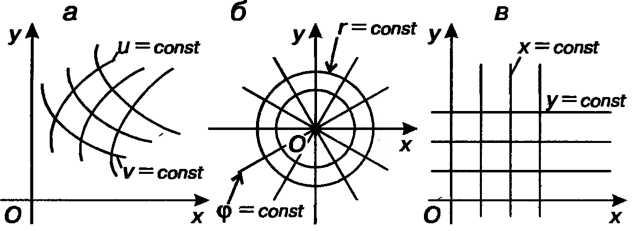
Рис. 19.8
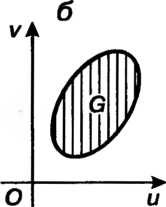
Замена переменных в двойных интегралах. Если непрерывно дифференцируемые функции (19.9) осуществляют взаимно однозначное отображение области  Плоскости
Плоскости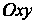 На область
На область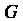 Плоскости
Плоскости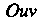 (рис. 19.9), то
(рис. 19.9), то
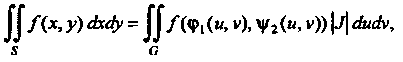 (19.10)
(19.10)
Где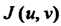 - функциональный определитель (якобиан):
- функциональный определитель (якобиан):
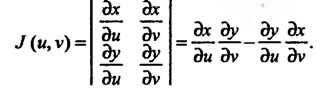
В случае перехода к полярным координатам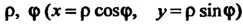 формула (19.10) принимает ввд
формула (19.10) принимает ввд
(19.11)
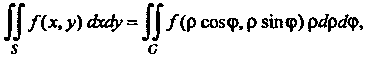 (19.12)
(19.12)
Так как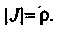
¦зот
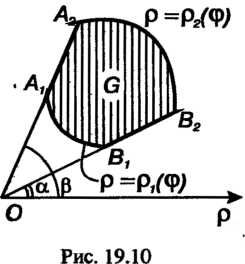
Если область (рис. 19.10) ограничена лучами, образующими с полярной осью углы
(рис. 19.10) ограничена лучами, образующими с полярной осью углы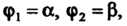 И кривыми
И кривыми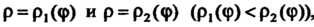 Го
Го
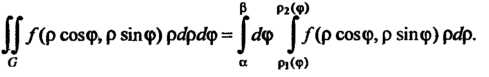 (19.13)
(19.13)
Если область Охватывает начало координат, то
Охватывает начало координат, то
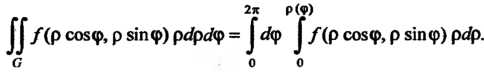 (19.14)
(19.14)
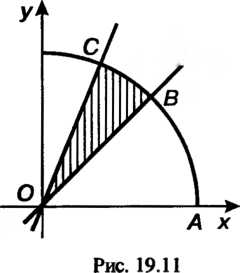
Пример 19.6. Вычислить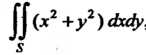 , где область
, где область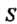 Ограничена.
Ограничена.
Линиями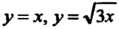 И дугой окружности
И дугой окружности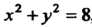 , лежащей в первой чет
, лежащей в первой чет
Верти (рис. 19.11).
Применим формулы (19.12), (19.13), предварительно выразив уравнения границ области и подынтегральную функцию в полярных координатах. Так как 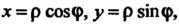 То уравнения границ области принимают вид pcos<p =
То уравнения границ области принимают вид pcos<p = 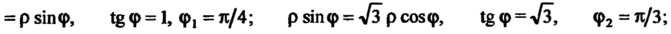
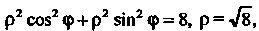 А подынтегральная функция
А подынтегральная функция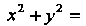
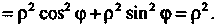 Следовательно,
Следовательно,
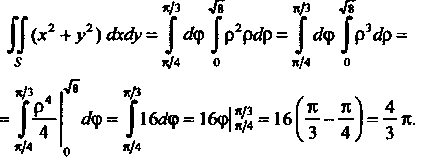
Пример 19.7. Вычислить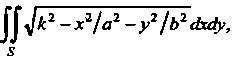 Где
Где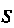 —область,
—область,
Ограниченная линиями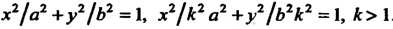
Для вычисления данного двойного интеграла введем так называемые обобщенные полярные координаты:

Найдем якобиан данного преобразования (считая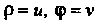 ). Так как
). Так как
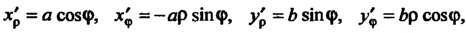 То, по формуле (19.11)
То, по формуле (19.11)
Получим
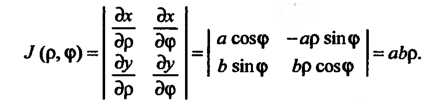
Подынтегральная функция и уравнения границ области S примут вид
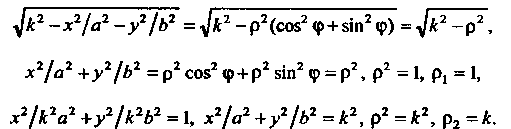
Итак, область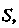 Ограниченную эллипсами, преобразование (I) переводит в другое кольцо, ограниченное окружностями радиусов
Ограниченную эллипсами, преобразование (I) переводит в другое кольцо, ограниченное окружностями радиусов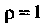 И
И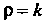 С центром в точке
С центром в точке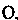 /угол
/угол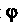 Меняется от
Меняется от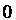 До
До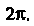 По формуле (19.14) находим
По формуле (19.14) находим
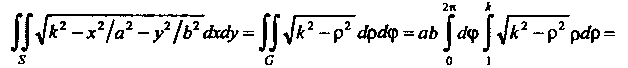
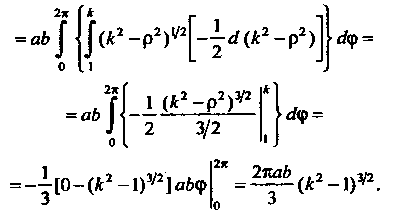
| < Предыдущая | Следующая > |
|---|