19.2. Вычисление двойного интеграла в декартовых прямоугольных координатах
Различают два основных вида области интегрирования:
1) область первого вида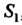 , т. е. область
, т. е. область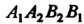 , ограниченную слева и справа прямыми
, ограниченную слева и справа прямыми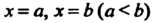 Соответственно, снизу - кривой
Соответственно, снизу - кривой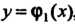 , сверху — кривой
, сверху — кривой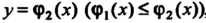 , каждая из которых пересекается с вертикалью
, каждая из которых пересекается с вертикалью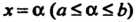 Только в одной точке (рис. 19.3);
Только в одной точке (рис. 19.3);
2) область второго вида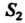 , т. е. область
, т. е. область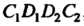 , ограниченную снизу и сверху прямыми
, ограниченную снизу и сверху прямыми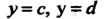 Соответственно, слева — кривой
Соответственно, слева — кривой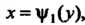 Справа
Справа
- кривой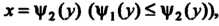 Каждая из которых пересекается с горизонталью
Каждая из которых пересекается с горизонталью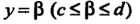 Только в одной точке (рис. 19.4).
Только в одной точке (рис. 19.4).
Замечание. В некоторых случаях точки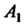 И
И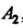 ,
,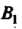 И
И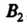 ,
,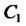 И
И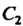 ,
,
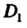 И
И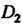 Могут сливаться в одну.
Могут сливаться в одну.
Если для функции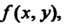 Определенной в области
Определенной в области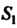 , существует двойной
, существует двойной
Интеграл, а при каждом постоянном значении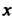 Из
Из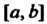 Простой интеграл
Простой интеграл
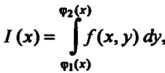
То существует также н повторный интеграл 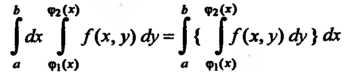 . и выполняется равенство
. и выполняется равенство
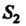
= | /(*, У) <Ь (19-4)
А Чг(У)
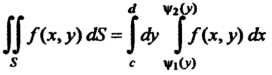
* С У^)
В предположении, что наряду с двойным интегралом существует определенный интеграл по х при постоянном у.
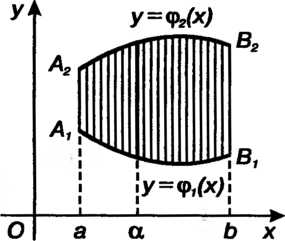
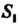
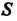
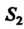
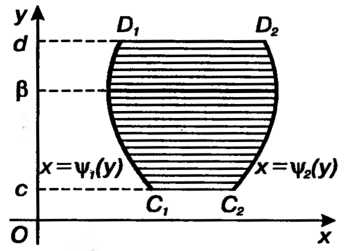
Рис. 19.3 . Рис. 19.4
Если область 5 можно рассматривать как область первого вида ¦У, и как область второго вида 52, то при выполнении указанных условий применимы обе формулы (19.3) и (19.4), поэтому
Ь <Ы*) а угОО
|<& | Ях, у)Оу = |ф |Дх, у)Ох.
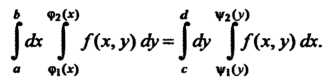
По этой формуле осуществляется изменение порядка интегрирования при вычислении соответствующего двойного интеграла.
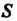
Пусть область 8 является прямоугольником со сторонами, параллельными осям координат, причем айхйЪ, сйу<0 (рис. 19.5), обозначим его так: 5 = [а, Ь; с, О].
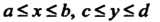
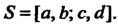
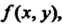
Если функция /(х, у), удовлетворяет в этом прямоугольнике условиям, о которых говорилось выше, то
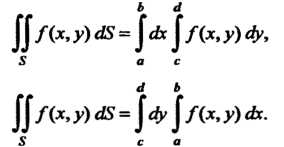
Ь л
Л /(х, >-) сК = |йх | /(*, у) Оу, (19.5)
(19.6)
Если функция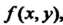 Интегрируемая в прямоугольнике
Интегрируемая в прямоугольнике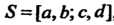 , может
, может
Быть представлена в виде произведения функции только от дс на функцию только от>>: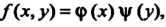 То
То
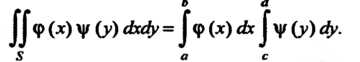
(19.7)
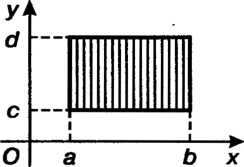
Рис. 19.5
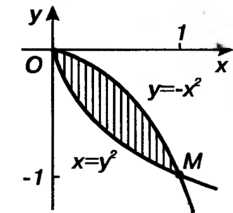
Рис. 19.6
Пример 19.2. Вычислить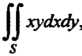 , где область
, где область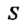 Является
Является
Прямоугольником [4,8; 1,2].
Задача сводится к вычислению повторного интеграла с помощью формулы (19.5). По этой формуле интегрирование выполняется сначала по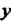 , в пределах от
, в пределах от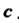 До
До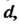 при произвольном постоянном
при произвольном постоянном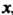 J а потом по
J а потом по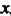 У в пределах от
У в пределах от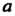 До
До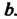 Формула (19.5) в данном случае принимает вид
Формула (19.5) в данном случае принимает вид
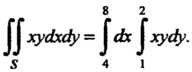
Так как
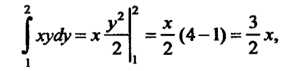
То
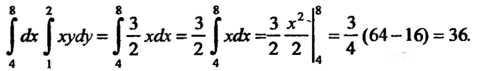
Следовательно,
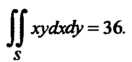
Замечание. Тот же результат можно получить и по формуле (19.6).
Действительно,
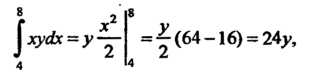
Л О 4.
| Оу |хуйх = 124^ = 12>-2|* = 12 (4 -1) = 36.
1 4 1
Пример 19.3. Вычислить ДОхгуДхс1у, 8 - область, ограниченная
Поэтому
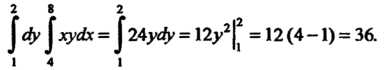
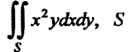
Ли
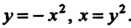
Ниями у = - х2, х = у2.
Данные линии пересекаются в двух точках 0(0,0), М(1,-1) (рис. 19.6). Область 5 можно рассматривать как область первого вида 5] и как область второго вида &2-Рассматривая ее как область первого вида, получаем следующие пределы интегрирования а = 0, Ь = \,у = ф,(лг) = -->/х, у = (р2(х) = - х2. По формуле (19.3) имеем
I ~х2
^х2ус! хс1у = ^сЬс ^x2у(^у.
5 0 -*]х
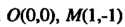
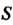
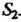

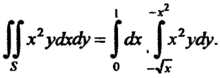
Так как
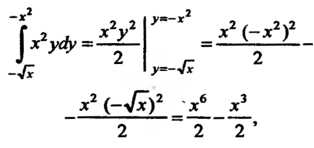
То
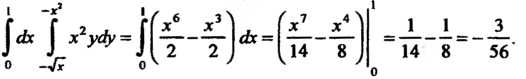
Следовательно, ДО х2ус1хс1у = -
}л }
О - V? О4 ' 4 '
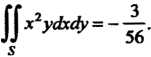
Замечание. Рассматривая данную область как область второго вида, находим следующие пределы интегрирования: с =—1, с/ = 0, х = у,(.у) = .у2,
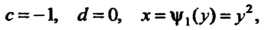
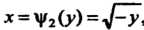
Х = 'Ц2(у)-4~У' поэтому
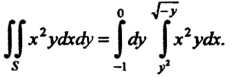
5 -1 /
Вычислив повторный интеграл, получим тот же результат.
О 4~У ДОх2у<&ф = ^е^у |х2ус1х.
Прямоугольник [1,3; 2,4].
Подынтегральная функция представляет собой произведение функции только от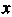 на функцию только от
на функцию только от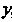 ,т. е.
,т. е.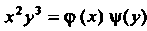 , где
, где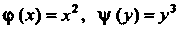 , поэтому
, поэтому
При вычислении двойного интеграла можно пользоваться формулой (19.7):
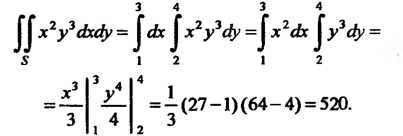
Пример 19.5. Вычислить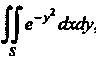 , где
, где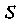 -
-
Треугольник с вершинами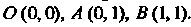
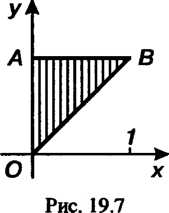
Данная область ограничена прямыми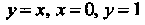 (рис. 19.7). Рассматривая ее как область первого вида, находим
(рис. 19.7). Рассматривая ее как область первого вида, находим
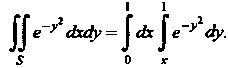
Интеграл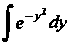 Является «неберугцимся» интегралом.
Является «неберугцимся» интегралом.
Мы не можем выразить его через элементарные функции. Поменяв порядок интегрирования, получим
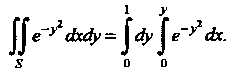
То
Так как
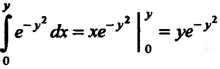
I
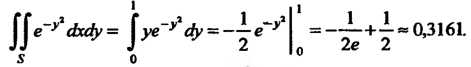
| < Предыдущая | Следующая > |
|---|