19.1. Понятие двойного интеграла, его геометрический и механический смысл
На плоскости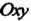 Рассмотрим область
Рассмотрим область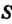 Площади
Площади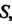 Ограниченную замкнутой кривой
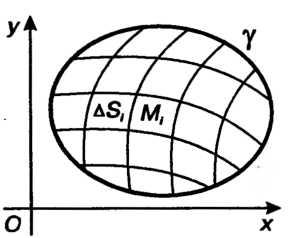
Ограниченную замкнутой кривой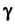 (рис 19.1). Пусть в области,
(рис 19.1). Пусть в области,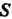 Определена функция
Определена функция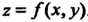 . Разобьем область
. Разобьем область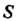 Сетью
Сетью
Линий на конечное число областей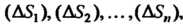 Площади которых
Площади которых
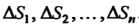 . В каждой
. В каждой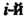 Элементарной области
Элементарной области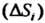 Выберем произвольную
Выберем произвольную
Точку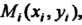 Значение функции в этой точке
Значение функции в этой точке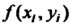 Умножим на площадь
Умножим на площадь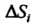
Соответствующей области и все произведения сложим. Полученная сумма
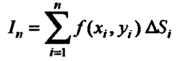
Называется интегральной суммой функции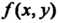 В области
В области
Двойным интегралом от функции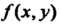 По области
По области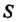 Называется конечный
Называется конечный
Предел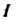 Интегральной суммы
Интегральной суммы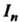 При
При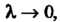 Где
Где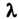 - наибольший из диаметров элементарных областей
- наибольший из диаметров элементарных областей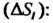
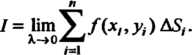
(19.1)
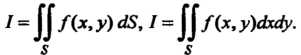
Обозначения двойного интеграла: I = ДО /(х, у) <18,1 = ДО/(х, у)сЫу.
5 5
Функция 2 = /(х, у), для которой предел (19.1) существует и конечен, называется интегрируемой.
Если функция 2 = /(х, у) непрерывна в области 8, то она. интегрируема в этой области.
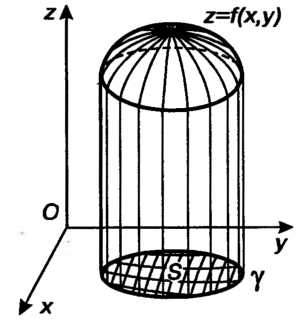
Геометрический смысл двойного интеграла. Если /(х, у)>0, то двойной интеграл от функции г = Дх, у) по области 8 равен объему тела, ограниченного сверху поверхностью г = /(х, у), с боков - цилиндрической поверхностью, образующие которой параллельны оси Ог, а направляющей служит контур у фигуры 8, снизу - плоскостью г = 0 (рис 19.2).
Механический смысл двойного интеграла. Двойной интеграл от функции г-Дх, у) > О по области 8 представляет собой массу фигуры 5, если подынтегральную функцию /(х, у) считать плотностью этой фигуры в точке М(х, у).
Свойства двойного интеграла.
1 • ДО с/(х, у) <18 = сДО Дх, у) 08 (с = сопз1).
2. Я<д* . у) ± (Ф (*. у))08 = ДО Дх, у) <18 ±ДОф (X, у) (18.
3. Если Дх, у) < ф (х, у), то ДО Дх, у) <18 < ДОф (х, у) <18.
4- ДО/(х, у)Л5 <ДО|/(х, у)|<й.
5- ДО /(*, У) 08 = ДО /(х, у) <18 +ДО Дх, у)
Где 5, и 82 — области, на которые разбита область 8.
6. Если в области 8 т< Дх, у) < М, то
ТЗ < ДО Дх, у)<18< М8, (19.2)
Откуда

Пример 19.1. Оценить двойные интегралы
/ _ ГГ 1 _ ГГ__
’ " д/25-х2-/ ’ 2 " 25+зт2(х+.у) + соя2у’
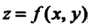
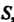
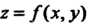
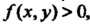
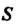
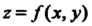
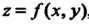
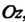
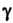
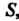
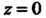

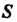
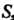
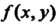
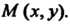
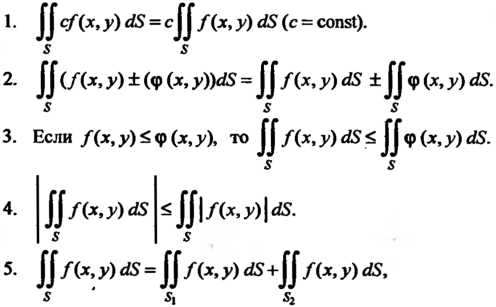
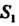
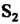
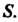
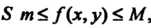
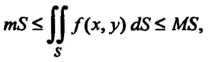
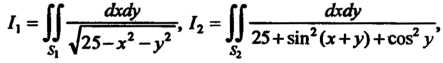
Где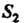 - квадрат
- квадрат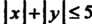
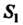 - круг
- круг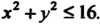
Оценим первый интеграл. Областью интегрирования является круг радиуса 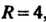 , площадь которого
, площадь которого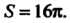 Так как в данной области функция
Так как в данной области функция
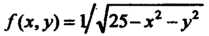 Удовлетворяет соотношениям
Удовлетворяет соотношениям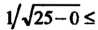
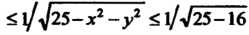 , т. е.
, т. е.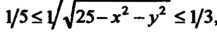 , то в соответствии
, то в соответствии
С неравенствами (19.2) получаем (16/5)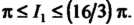
Переходим к оценке второго интеграла Областью интегрирования является квадрат с вершинами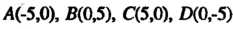 . Длина его стороны
. Длина его стороны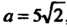 , а площадь
, а площадь
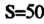 '. Поскольку
'. Поскольку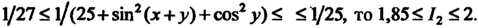
| < Предыдущая | Следующая > |
|---|