18.11. Семейства линий и их огибающие. Семейства поверхностей и их огибающие
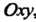
Однопараметрическим семейством линий, лежащих в плоскости Оху, называется множество линий, определяемое уравнением
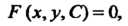
Р(х, у,С) = 0, (18-32)
В котором параметр С может принимать различные действительные значения (при каждом фиксированном значении С получаем определенную линию семейства).
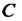
Огибающей семейства линий называется такая линия, которая в каждой точке касается некоторой линии семейства.
Множество всех точек, удовлетворяющих системе уравнений
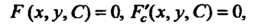
Р(х, у,С) = 0,Щх, у,С) = 0, (18.33)
Называется дискриминантной линией семейства (18.32).
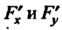
Если в точках дискриминантной линии частные производные Р^мРу
Одновременно в нуль не обращаются, то дискриминантная линия совпадает с огибающей семейства.
Множество линий, определяемое уравнением
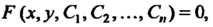
Р(х, у,С1,Сг,...,С„) = 0,
Где С,,С2,...,СВ - независимые параметры, называется «-параметрическим семейством линий (параметры называются независимыми или существенными, если их число нельзя уменьшить путем введения новых параметров).
Однопараметрическим семейством поверхностей называется множество поверхностей, определяемое уравнением
Огибающей семейства поверхностей называется поверхность, которая в каждой своей точке касается некоторой поверхности семейства
Огибающая семейства поверхностей (18.34) удовлетворяет системе уравнений
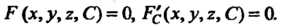(18.35)
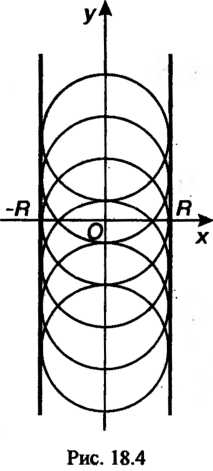
Пример 18.14. Найти огибающую однопараметрического семейства линий
Система уравнений (18.33) запишется так:
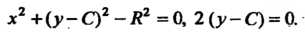
Из этой системы находим, что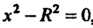 
, или.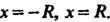
Прямые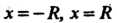
Являются огибающей
Данного однопараметрического семейства линий — множества окружностей радиуса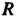
С центрами на оси
(рис 18.4).
Пример 18.151 Найти огибающую однопараметрического семейства поверхностей
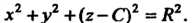
Система уравнений (18.35) принимает вид
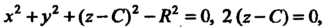
Откуда следует, что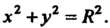
Круговой цилиндр радиуса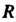
, ось которого совпадает с осью
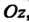, является огибающей данного однопараметрического семейства сфер радиуса
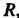Центр каждой из которых находится на оси
| < Предыдущая | Следующая > |
|---|
