18.10. Касательная плоскость и нормаль к поверхности
Касательной плоскостью к поверхности в данной точке М (точке касания) называется плоскость, в которой лежат касательные в этой точке к всевозможным кривым, проведенным на данной поверхности через указанную точку.
Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке касания. Координаты вектора нормали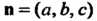
К поверхности
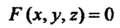(18.29)
В точке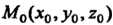
Пропорциональны значениям соответствующих частных
Производных функции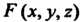
В этой точке:
,
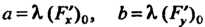Где
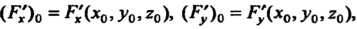
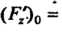
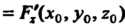L \
Координаты вектора п входят в уравнение касательной плоскости к поверхности в точке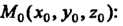
(18.30)
А также в уравнение нормали к данной поверхности в той же точке:
Х-х0 _У~Уо _г-20
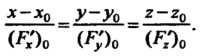
Пример 18.13. Записать уравнения нормали и касательной плоскости к поверхности г = х2+у2 в точке М0( 1,-2,5).
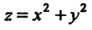
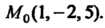
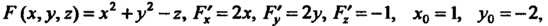
Поскольку Р(х, у,г) = х2 +у2-г, Р’ = 2х, Р' = 2у, Р2‘ = -1, х0 = 1, у0=-2, 20 = 5, Р'(х0, у0, г0) = 2, Р'(х0, у0,20) = -4, то на основании уравнений (18.30), (18.31) получаем 2 (х -1) - 4 (_у+2) - (г - 5) = 0, 2х-4у-г-5=0 (уравнение
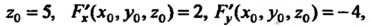
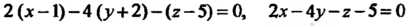
Касательной плоскости), ——- = ^+2 = ——- (уравнения нормали). 2-4-1
| < Предыдущая | Следующая > |
|---|
