18.09. Условный экстремум

 

Если разыскивается экстремум функции многих переменных, которые связаны между собой одним или несколькими уравнениями (число уравнений должно быть меньше числа переменных), то говорят об условном экстремуме. При решении задачи можно пользоваться методом неопределенных множителей Лагранжа.

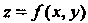
Чтобы найти условный экстремум функции г = /(х, у) при наличии уравнения связи <р(х, _у) = 0, составляют функцию Лагранжа

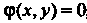
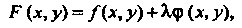
Г (*, У) = /С*, У) + *-Ч> (х, у),  (18.26)

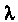
Где X - неопределенный постоянный множитель, и ищут ее экстремум. Необходимые условия экстремума функции (18.26) выражаются системой трех уравнений с тремя неизвестными дс, у, X:

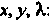
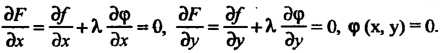
= ф(х, у) = 0. 08.24

Дх дх дх дУ ду ду

Вопрос о существовании и характере условного экстремума решается на основании изучения знака второго дифференциала функции Лагранжа 42Р = Р"еЬс2 +2Р"<1хс^+ Р'^Лу2 для испытуемой системы значений дс, у, X, полученной из системы (18.27) при условии, что с/х и Лу связаны уравнением

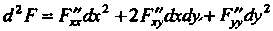
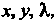
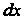
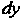
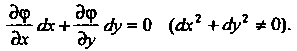
^¦ек+^-ау = 0 (0х2+0у2*0).

Эл ду

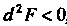
Функция /(х, у) имеет условный максимум, если Л2Р < 0, и условный минимум, если й2Р> 0.

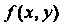
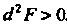
Аналогично находится условный экстремум функции трех или большего числа переменных при наличии уравнений связи.

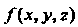
Если, например, требуется найти экстремум функции /(дс, у, г) при условиях

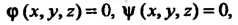
Ф (дс, у, г) = 0, у (дс, у, г) = 0,  (18.28)

То вводят функцию

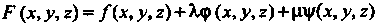
Р (дс, у, 2) = /(дс, у, 2)+Х<р (дс, у, г)+цу(дс, У, *)

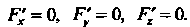
Икуравнениям(18.28)присоединяютещетри уравнения: Рх = 0, Р' = О, Р' = 0.

Пример 18.12. Найти экстремум функции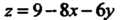При условии,

Чтоее аргументы удовлетворяют уравнению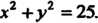

Геометрически задача сводится к нахождению экстремальных значений аппликаты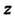Точек пересечения плоскости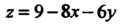С круговым цилин

Дром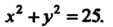

Составляем функцию Лагранжа, определяемую формулой (18.26):

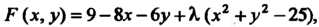Находим ее частные производные 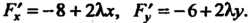Система уравнений (18.27) принимает ввд

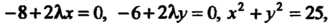
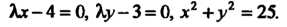
Решив эту систему, получим: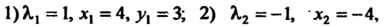

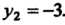. Находим вторые частные производные: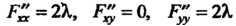И

Второй дифференциал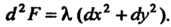Так как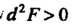При

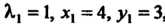, то функция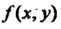В точке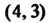Имеет условный минимум,

Причем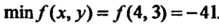. Поскольку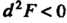При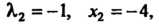

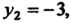То в точке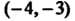Функция имеет условный максимум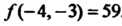

< Предыдущая		Следующая >