18.08. Экстремум функции нескольких переменных

 

Максимумом (минимумом) функции 2 = /(х, у) в точке М0(х0,у0) называется такое ее значение /(х0,у0), которое больше (меньше) всех других ее значений, принимаемых в точках М(х, у), достаточно близких к точке М0 и отличных от нее.

Максимум и минимум функции называется ее экстремумом. Точка, в которой достигается экстремум, называется точкой экстремума.

Экстремум функции трех и большего числа переменных определяется аналогично. Необходимые условия экстремума. В точке экстремума дифференцируемой функции нескольких переменных частные производные ее равны нулю.

Если М0(х0,у0) - точка экстремума дифференцируемой функции г =Лх, у), то

/;(*о. Уо) = 0, /;(х0,у0) = о.  (18.20)

-Из этой системы уравнений находятся стационарные точки. Система (18.20) эквивалентна одному уравнению

4Г(хо, Уо) = 0.  (18.21)

В общем случае в точке экстремума Л/0(х0,з/0) функции г = /(х, у) выполняется равенство (18.21) или с!/(х0,у0) не существует.

Достаточные условия экстремума. Пусть М0(х0,у0) - стационарная точка,

Т. е. точка, для которой выполняется равенство (18.21):

1)если

<*2/С*о. У о ) < 0 (при Ох1 + <1у2 > 0),  (18.22)

То /(,х0,у0) - максимум функции г = /(х, у);

2)если

42/(х0, у0) > 0 (при Ох2 +<1у2 > 0),  (18.23)

То /(х0,у0) — минимум функции 2 = /(х, у).

Эти условия эквивалентны следующим: пусть /х(х0,у0) = 0, /у(х0,у0) = 0 и А = /"(х0,у0), В = /"(х0,у0), С = /"(х0,у0),  (18.24)

Д = АС-В2,  (18.25)

Тогда:

1)  если Д>0, то функция / (х, у) имеет экстремум в точке М0: максимум при А< 0 (или С < 0), минимум при А > 0 (или С > 0);

2)  если Д < 0, то экстремума в точке М0 нет.

Для функции трех и большего числа переменных необходимые условия экстремума аналогичны условиям (18.20), а достаточные условия аналогичны условиям (18.22), (18.23).

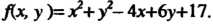
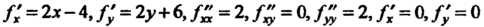
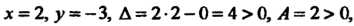
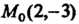
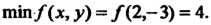
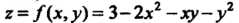
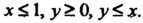
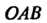
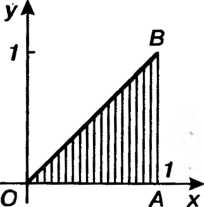
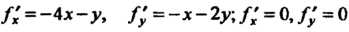
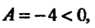
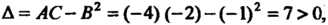
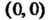
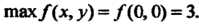
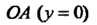
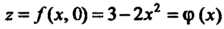
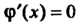
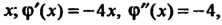
Рис. 18.3

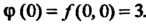
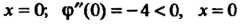
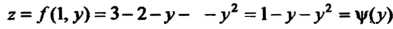
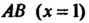
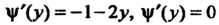
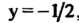
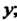
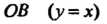
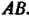
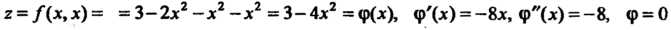
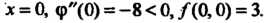
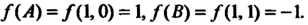
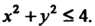
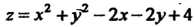
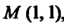
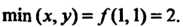
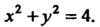
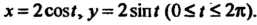
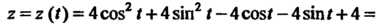
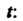
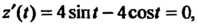
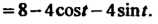
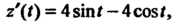
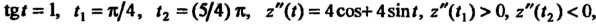
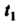
Пример 18.9. Найти экстремум функции Дх, у )= х2+ у2- 4х+6у+17.

Поскольку /; = 2х-4,/; = 2у+6,/" = 2,/" = 0,/"=2,/; = 0,/; = 0 при

Х = 2, у = -3, А = 2-2-0=4>0, А = 2> О, то в точке М0(2,-3) функция имеет минимум, причем тт/(х,.у) = /(2,-3) = 4.

Пример 18.10. Найти наибольшее и наименьшее значения функции г = /(х, у) = 3-2х2-ду-у2 в замкнутой области, заданной системой неравенств: х < 1, у> 0, у<х.

Область представляет собой треугольник ОЛВ (рис. 18.3), причем О (0,0), А (1,0), 5(1,1). Находим экстремум

Функции: /; = -4 х-у, /; = ~х - 2у; /' = 0, /’ = 0

При х = 0, у = 0;/" = -4,/; = /; = -1,/; = -2,

А = АС-В2 = (-4)(-2)-(-1)2 =7>0, Л = -4<0, в точке (0,0) функция достигает максимума: шах /(х, у) = /(0,0) = 3. Найдем экстремумы на границе области: на стороне ОА (у = 0) функция 2 = /(х, 0) = 3 - 2х2 = ф (х) зависит от одной переменной х; ф'(х) = —4х, ф"(х) = -4, ф'(х) = О при х = О, ф"(0) = - 4 < 0, х = 0 - точка максимума: ф (0) = /(0,0) = 3. На пря-мой АВ (х = 1) функция 2 = /(\,у) = 3-2-у - - у2 = 1-у-у2 = у (у) зависит только от у; \у'(у) = -1-2у, ф'(у) = 0при у = -1/2, но эта точка не принадлежит отрезку АВ. На стороне ОВ (у=х) функция зависит только от х: 2 = /(х, х) = =3-2х2-х2-х2 =3-4х2 =ф(х), ф'(х) = -8х, ф"(х) = -8, ф = О при х = 0, ф"(0) = —8 < 0, /(0,0) = 3. Вычисляем значения функции в точках А и В: /(А) = /(1,0) = 1, /(В) = /(1,1) = -1. Следовательно, в заданной области наименьшее значение данной функции равно -1, а Наибольшее равно 3.

Пример 18.11. Найти наибольшее и наименьшее значения функции 2 = х2+уг-2х-2|у+4 в круге х2 +у2 < 4.

Данная функция имеет минимум в точке М (1,1), лежащей в заданной области, причем шп(х, у) = /(1,1) = 2.

Исследуем изменение функции на границе области, т. е. на окружности х2 +у2 = 4. Воспользуемся параметрическими уравнениями этой окружности х = 2созГу>' = 25т<(0<<5 271). На данной окружности функция становится функцией одной переменной I: г = г(0 = 4соз21 + 4ып2/-4созГ -45ШГ + 4 = = 8-4соз*-4зтл Поскольку г'(/) = 4зт< —4соз<, 2'(<) = 4зт<-4соз< = 0, 1§/ = 1, /, = п/4, 12 = (5/4)7С, 2"(0 = 4соз+4зт<, 2"(<,)>0, г"(12)<0, то <, -

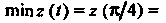
Точка минимума, (2 ~ точка максимума, причем шаг (/) = г (я/4) =

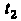
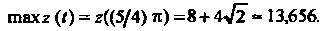
= 8-4^2 - 2,344, шах2 (0 = г((5/4) п) =8+4^2 -13,656.

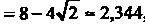
Рассматривая полученные экстремальные значения функции, заключаем, что в указанном круге наибольшее значение функции равно 8+4^=13,656, достигается оно в точке N (-2, -2), лежащей на границе окружности; наименьшее значение функции равно 2, достигается в точке минимума М (1,1).

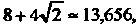
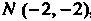
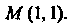
< Предыдущая		Следующая >