18.07. Дифференцирование неявных и сложных функций

 

Функция п переменных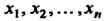Называется неявной, если она задана

Уравнением

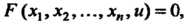(18.17)

Не разрешенным относительно и.

Частные производные неявной функции, заданной уравнением (18.17), находятся по формулам

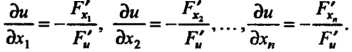
В частности, если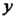- функция одной переменной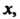Заданная

Уравнением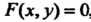, то

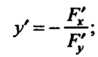(18.18)

Если г - функция двух переменных х, у, заданная уравнением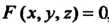, то

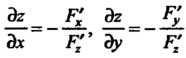
Если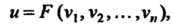Где,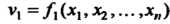

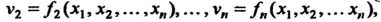То функция и называется сложной функцией независимых переменных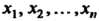. Переменные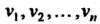Назы

Ваются промежуточными аргументами.

Частная производная-сложной функции по одной из независимых переменных равна сумме произведений ее частных производных поцфомежуточным аргументам на частные производные этих аргументов по данной независимой переменной:

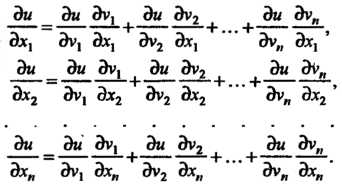
(18.19)

Если все промежуточные аргументы являются функциями одной независимой переменной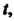То функция будет сложной функцией отПолная производная этой функции находится по формуле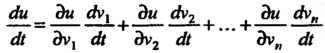

 

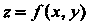
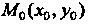
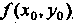
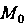
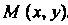
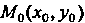
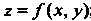
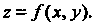
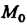
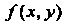
< Предыдущая		Следующая >