18.06. Частные производные и дифференциалы высших порядков. Формула Тейлора

 

Частные производные функции нескольких переменных называют также частными производными первого порядка или первыми частными производными.

Частными производными второго порядка (или вторыми частыми производными) данной функции называются соответствующие частные производные от ее первых частных производных.

Для функции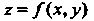По определению имеем

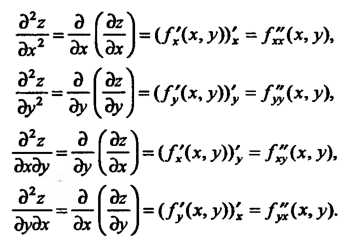
Вторые частные производные обозначаются также символами 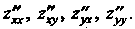Производные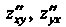Называются смешанными частными

Производными.

Частные производные появились в трудах И. Ньютона, Г. Лейбница, Я. Бернулли и И. Бернулли. Обозначения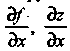Ввел Лежандр (1786),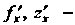

Ж. Лагранж (1797,1801),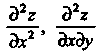- К. Якоби (1837).

Теорема 18.3. Если функция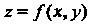И ее смешанные производные

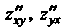Определены в некоторой окрестности точки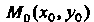И непрерывны в

Этой точке, то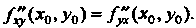

Дифференцируя частные производные второго порядка как по х, так и по у, получаем частные производные третьего порядка или третьи частные производные:

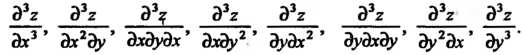
Вообще, частная производная л-го порядка функции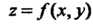Есть первая

Частная производная от ее частной производной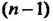-го порядка.

Аналогично определяются и вычисляются частные производные второго и высших порядков от функции трех и большего числа переменных.

Полным дифференциалом второго порядка некоторой функции называется полный дифференциал от ее полного дифференциала.

Полным дифференциалом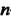-го порядка называется полный дифференциал от полного дифференциала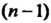-го порядка. Если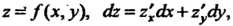То

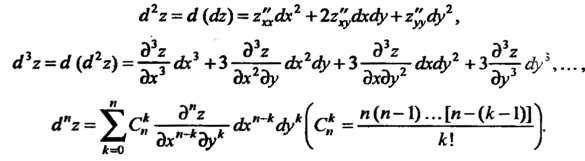
Эту формулу записывают и в следующем символическом виде:

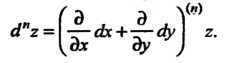
Формула Тейлора для функции двух переменных

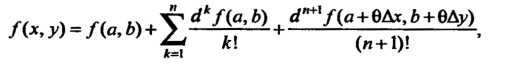(18.15)

Или

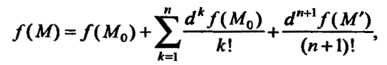(18.16)

Где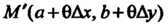- точка области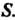

Формула Тейлора для функции большего числа переменных 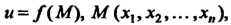Аналогична формуле (18.16).

Замечание. При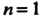Формула (18.15) принимает вид

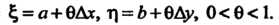
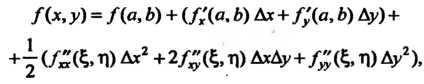
Пример 18.6. Дана функция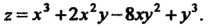Найти ее

Частные производные второго порядка. Находим сначала первые производные: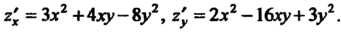

Пользуясь определениями и правилами дифференцирования, получаем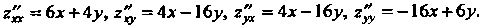

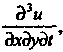
Пример 18.7. Дана функция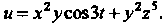Найти

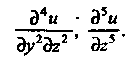
Дифференцируя по одной из переменных, считаем все другие постоянными:

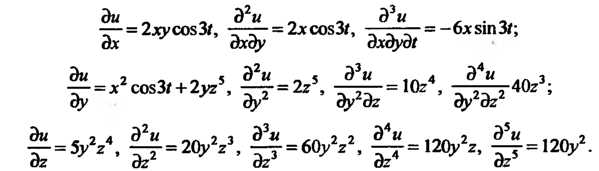
Пример 18.8. Дана функция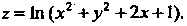Показать, что

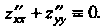
Найдем частные производные первого и второго порядка:

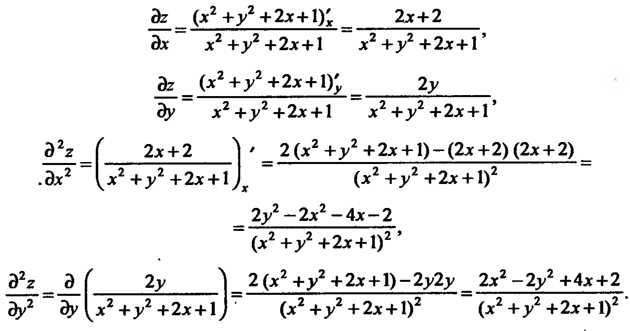
Составим сумму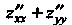Вторых частных производных и убедимся, что она

Тождественно равна нулю:.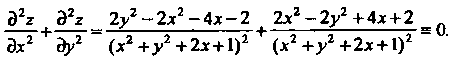

< Предыдущая		Следующая >