18.05. Полный дифференциал функции нескольких переменных

 

Если полное приращение функции г=/(х, у) в точке Мо(х0,уо) представимо в виде

Дг = РАх + ()Ау + еДр,

Где Р, () - постоянные, Др = д/дх2 + Ау2 и е—>0 при Др—>0, то РАх+()Ау называют полным дифференциалом данной функции в этой точке и обозначают через сЬ: сЬ= РАх + ()Ау. Следовательно,

Дг = йЬ+еДр, е —> 0 при Др —> 0.  (18.9)

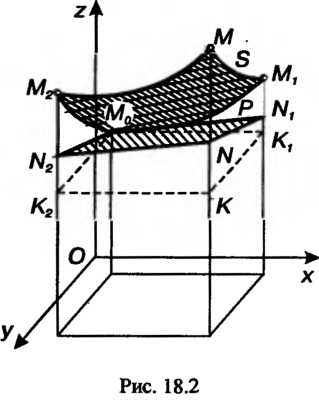
Полный дифференциал функции двух переменных равен приращению аппликаты г касательной плоскости в точке М0(х0, уи, г0) к поверхности, являющейся

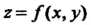
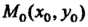
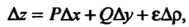
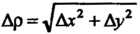
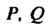
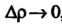
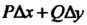
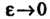
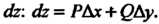
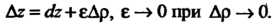
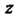
Функция, обладающая непрерывными частными производными, имеет полный дифференциал, причем

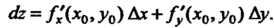(18.10)

Дифференциалы независимых переменных совпадают с их приращениями,

Т. е.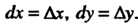

Полный дифференциал функции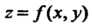Является функцией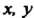При фик

Сированных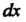И

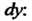
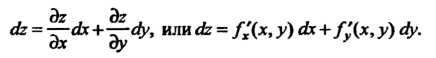
Графиком этой функции, когда аргументы х и у получают приращения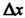И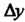 (рис 18.2,).

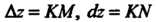Функция, имеющая полный дифференциал, называется дифференцируемой. Если функция дифференцируема в некоторой точке, то она и непрерывна в ней.

Из формулы (18.9) следует, что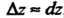, или

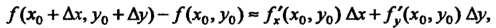(18.11)

Откуда  ,

Если все первые частные производные функции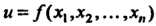Непрерыв

Ны, то полный дифференциал выражается формулой

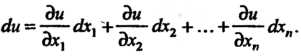(18.13)

Каждое слагаемое правой части этой формулы называется частным дифферециалом.

В частности, полный дифференциал функции трех переменных вычисляется по формуле

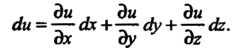(18.14)

Пример 18.2. Дана функция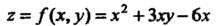И две точки

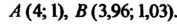Требуется: 1) вычислить значение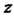Функции в точке В; 2)

Вычислить приближенное значение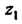Функции в точке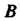Исходя из значения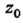

Функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом.

Вычисляем значения данной функции в точках А и В:

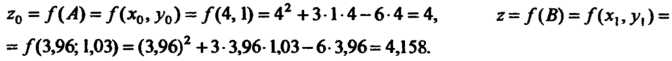
Находим приращения аргументов: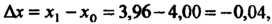

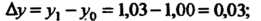Значения частных производных 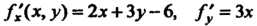В точке А: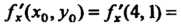

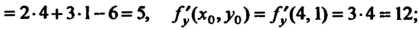Значение дифференциала в точке А по формуле (18.10):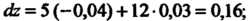Значение функции в

Точке В по формуле (18.12):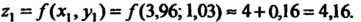

Пример 18.3. Вычислить приближенно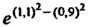

Рассмотрим функцию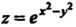. Искомое число можно считать приращенным

Значением этой функции приПоскольку

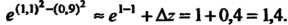
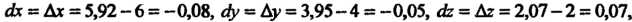
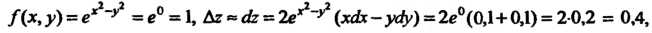
Пример 18.4. Вычислить полный дифференциал функци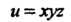иПри

Переходе от точки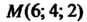К точке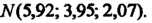

Так как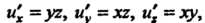То в соответствии с формулой (18.14)

Подставив в эту формулу значения,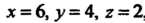

Получим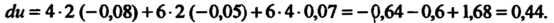

Пример 18.5. Как изменится диагональ прямоугольника со сторонами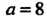 см,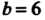См, если сторону а уменьшить на 3 мм, а сторону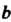Увеличить на 7 мм?

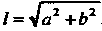Введем в рассмотрение функцию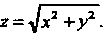Поскольку

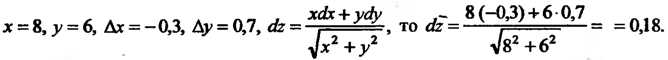
Следовательно, диагональ увеличится на 0,18 см.

< Предыдущая		Следующая >