18.04. Частные производные функции нескольких переменных

 

Частной производной функции нескольких переменных по одной из них в фиксированной точке называется предел отношения соответствующего частного приращения этой функции к приращению данной переменной, когда последнее стремится к нулю.

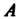
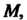
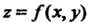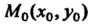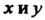Для функцииЧастные производные в точкеПоСо

Ответственно определяются формулами:

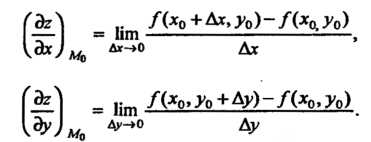
Употребляются и другие обозначения: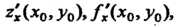

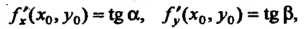
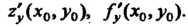
Частная производная функции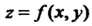По переменной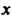Выражает скорость

Изменения функции в данном направлении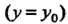Или скорость изменения

Функции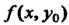Одной переменной.

Частные производные функции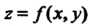Имеют следующую геометриче

Скую интерпретацию:

Где а - угол между осью Ох и касательной в точке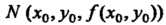К линии

Пересечения поверхности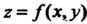И плоскости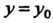,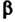- угол между осью

Оу и касательной в той же точке к линии пересечения данной поверхности с плоскостью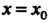(рис 18.1).

Очевидно,

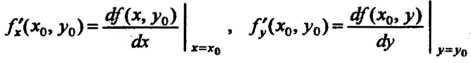
Т. е. частная производная в данной точке равна производной функции одной переменной, вычисленной при соответствующем значении аргумента, поэтому при нахождении частных производных пользуются обычными правилами дифференцирования.

При переходе от точки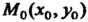К точке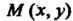Получим новые значения

Частных производных. Следовательно, частные производные функции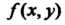 также являются некоторыми функциями двух переменных:

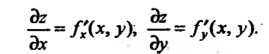
Пример 18.1. Найти значения частных производных функции

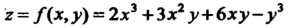В точке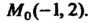

 

Считая у

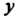
Постоянной и дифференцируя г, как функцию х, находим

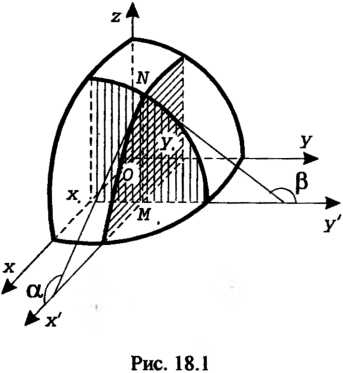
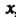
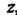
Рис. 18.1

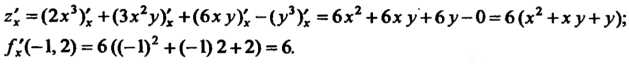
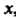
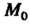
Частную производную по х, вычисляем ее значение в точке М0: г' = (2х3)' +(3х2у)'х +(6ху)'х -(у3)' = 6х2 + 6ху + 6у-0 = 6(х2 +ху + у);

/*'(-1,2) = 6 ((-1)2 + (-1) 2 + 2) = 6.

Считая х постоянной и дифференцируя г, как функцию у, находим частную производную по у и ее значение в точке М0:

2; =(2х3Уу+(Зх2уУу+(6хуУу -(уъУу = 0 + Зх2 + 6х - Зу2 = 3 (х2 + 2х - у2); /Д-1,2) = 3 ((-1)2+ 2(- 1) - 22) = -15.

 

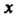
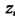
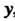
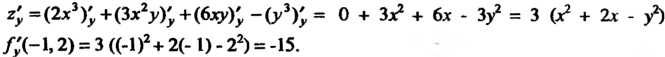
< Предыдущая		Следующая >