18.03. Предел и непрерывность функции нескольких переменных
Полное приращение функции двух переменных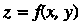
В точке
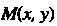Опре
Деляется формулой
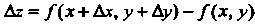(18.3)
А ее частные приращения (по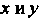
Соответственно) в той же точке — формулами
(18.4)
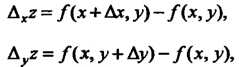(18.5)
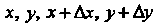Принадлежат области определения функции.
Аналогично определяются полное и частные приращения функции большего числа переменных.
Замечание. Частное приращение функции по одному из аргументов есть разность между двумя ее значениями, когда приращение получает только данный аргумент; полное прйращение функции - разность между двумя значениями, когда приращения получают все ее аргументы.
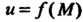
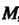
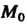
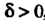
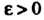
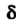
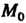
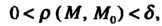
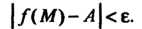
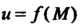
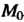
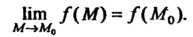
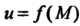
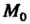
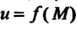
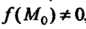
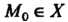
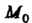
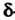
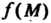
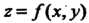
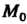
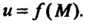
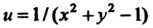
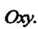
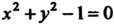
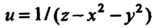
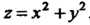
Число А называется пределом функции и = ДМ) при М, стремящемся к М0,если для любого е>0 существует. такое 8 > 0, что при всех М, расстояние которых до точки М0 меньше 5, т. е.
О <р(М, М0)<8, (18.6)
Выполняется неравенство
|/(М)-Л|<е. (18.7)
Функция и = ДМ) называется непрерывной в точке М&, если выполняется условие
11ш ДМ) = ДМ0). (18.8)
М->м0
Необходимое и достаточное условие непрерывности функции и = /(М) в точке М0 выражается равенством
Нш Ды = 0, или Ит (ДМ)-/(М0)) = 0,
Др-»0 Ар—>0
Где Др = р(М, М0), Ди = /(М)-ДМ0).
Теорема 18.1. (об устойчивости знака непрерывной функции).
Если функция и = /(М) непрерывна в точке М0 е X и /(М0)*0, то существует Ь-окрестностъ точки М0, в которой /(М) не обращается в нуль и имеет знак, совпадающий со знаком ДМ0).
Теорема 18.2. Если функция г = /(х, у) непрерывна в ограниченной замкнутой области, то она ограничена в этой области и достигает в ней своего наименьшего и наибольшего значения.
Если в некоторой точке М0 не выполнено условие (18.8), то эта точка называется точкой разрыва функции и = ДМ).
Точки разрыва функции двух переменных могут заполнять отдельные линии (линии разрыва). Например, для функции и = 1/(х2 +у2-1) линией разрыва является окружность х2 +>>2 -1 = 0 в плоскости Оху. Точки разрыва функции трех переменных могут заполнять отдельные поверхности (поверхность разрыва). Так, для функции и=1/(г-х2 - у2) поверхностью разрыва является параболоид вращения г = х2+у2.
| < Предыдущая | Следующая > |
|---|
