18.01. Множества в /7-мерном пространстве
Упорядоченную совокупность п действительных чисел х1,х2,...,х„ называют точкой, а сами эти числа - ее координатами. Запись М (х,, х2,,хп) означает, что точка М имеет координаты х,,х2,...,хя. Множество всевозможных точек называется арифметическим (координатным) и-мерным пространством и обозначается символом А" или А„.
Арифметическое /г-мерное пространство А" называется /г-мерным евклидовым пространством, если для любых двух точек М '(*,', хг' М"(х,", х%,... ,х'0,
Принадлежащих А”, определено расстояние по формуле
Р(М\ М") = х’)2 + «-х'2)2 +... + х'п)г.
Евклидово /г-мерное пространство обозначается через Е” или Е„.
Примеры множеств в /г-мерном евклидовом пространстве Е".
1. Если для координат всех точек множества {м) выполняется неравенство р (М, М0)< К, или
(х, - х,0)2 +(х2 - х20)2 +-.+(*,-х?,)2 < К2, то {М} называется открытым/г-мерным шаром.
2. Множество {М} точек М (х,, х2,...,хя), координаты которых удовлетворяют неравенству р (М, М0) < Л, или
(х, - х,0)2 +(х2 - х20)2 +...+(х„ - х„0)2 < К2, называется замкнутым /г-мерным шаром радиуса К с центром в точке М0(х1°,х2°,...,х°).
3. Множество {М} точек Л/ (х,, х2,... ,х„ ), для которых р(М, М0)=К, или
(х, - х,0)2 +(х2 - х20)2 + ... + (х„ - х„0)2 = К2, называется (/г -1) - мерной сферой радиуса К с центром в точке М0(х1°,х2°,...,хя0).
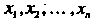
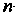
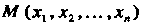
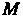
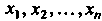
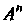
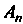
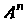
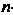
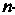
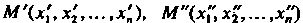
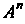
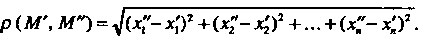
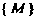
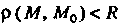
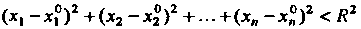
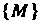
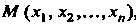
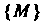
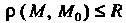
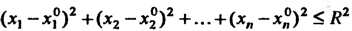
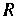
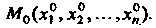
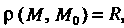
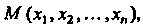
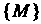
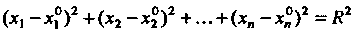
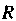
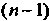
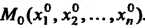
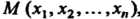
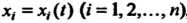
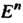
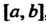
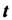
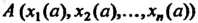
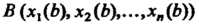
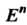
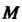
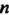
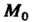
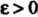
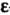
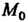
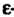
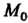
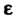
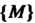
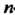
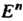
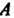
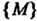
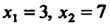
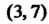
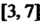
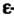
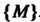
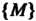
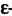
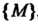
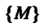
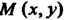
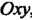
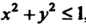
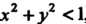
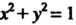
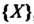
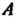
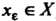
4. Множество точек М (х,,х2,...,х„), координаты которых заданы как непрерывные функции х! = х,(1) («= 1,2,..., п), определенные на некотором отрезке [о, А], называется непрерывной кривой в пространстве Е". Аргумент I называется параметром кривой. Точка А (х1(а),х2(а),...,хл(а>) называется началом, точка В (х1(Ь),х2(Ь),...,х„(Ь)) - концом данной кривой.
Множество точек М л-мерного евклидова пространства Е", для каждой из которых расстояние до фиксированной точки М0 меньше е > О, называется е-окрестностью точки М0. Другими словами, е-окрестностью точки М0 называется и-мерный открытый шар радиуса е с центром в точке М0.
Пусть {М} - некоторое множество точек «-мерного евклидова пространства
Е”. Точка А называется предельной точкой (или точкой сгущения) множества {М}, если любая ее окрестность содержит по крайней мере одну точку этого множества, отличную от А. Предельная точка может принадлежать или не принадлежать ему. Например, точки х, = 3, х2 = 7 являются предельными для отрезка [3,7] и интервала (3,7), но первому они принадлежат, а второму не принадлежат. Множество, содержащее все свои предельные точки, называется замкнутым. Если существует окрестность точки В множества {М} , не содержащая никаких других точек этого множества, кроме самой точки В, то эта точка называется изолированной точкой множества {М} .
Точка М множества {М} называется внутренней точкой этого множества, если существует такая ее е-окрестность, все точки которой принадлежат множеству {М}. Открытым множеством называется множество, все точки которого внутренние. Множество называется связным, если любые две его точки можно соединить в нем непрерывной кривой. Областью называется открытое связное множество. Точка М называется граничной точкой множества {М}, если любая ее Е-окрестность содержит как точки множества { М}, так и точки, не принадлежащие ему.
Совокупность всех граничных точек множества {М} называется его границей. Если к области присоединить его границу, то полученное множество называется замкнутой областью. Например, множество точек М (х, у) плоскости Оху, для
Которых х2 +у2 < 1, является замкнутой областью; к области, определяемой неравенством х2 + у2 < 1, присоединены все его граничные точки, т. е. точки окруж-ности х2+у2 = 1. .
Множество называется ограниченным, если все его точки находятся внутри некоторого и-мерного шара.
Диаметром ограниченного множества {М} называется верхняя грань расстояний между его любыми двумя точками.
Число А называется верхней гранью числового множества {Х}, если: 1) х < А для всех х е X; 2) для любого числа е > 0 существует такое хе е X, что
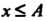

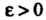
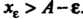 . Верхняя грань множества
. Верхняя грань множества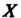 Обозначается через
Обозначается через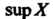 Или
Или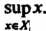 Например, для сегмента
Например, для сегмента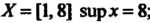 I для интервала
I для интервала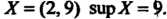
Число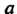 Называется нижней гранью числового множества
Называется нижней гранью числового множества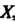 , если:
, если:
1)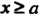 Для всех
Для всех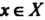 ; 2) для любого числа
; 2) для любого числа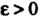 Существует такое
Существует такое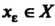 , что
, что
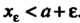 . Нижняя грань множества
. Нижняя грань множества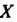 Обозначается через
Обозначается через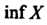 Или
Или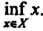 На
На
Пример, если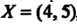 , то
, то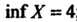 ; если
; если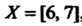 , то
, то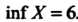
Всякое непустое множество действительных чисел, ограниченное сверху, имеет конечную верхнюю грань, а ограниченное снизу - конечную нижнюю грань. У всякого множества действительных чисел верхняя (нижняя) грань единственна.
| < Предыдущая | Следующая > |
|---|