17.9. Объем тела. Площадь поверхности вращения

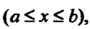
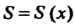
Если задана функция 5 = 5 (х) (а<х< Ь), определяющая площадь поперечного сечения тела плоскостью, перпендикулярной оси Ох, то его объем вычисляется по формуле

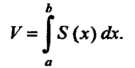
(17.38)

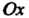
Объем тела, полученного вращением вокруг оси Ох криволинейной трапеции АаЪВ (рис. 17.17), где АВ - дуга кривой у = /(х), вычисляется по формуле

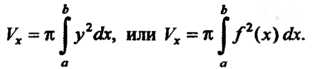
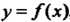
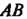
(17.39)

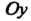
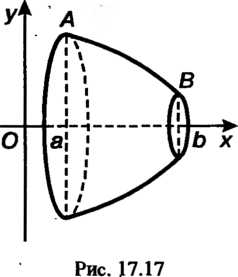
Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции СссЮ (рис. 17.18), где СО - дуга кривой х = ф(.у), определяется формулой а  ь

1^ = 71:^х2ф, или Уу = 711 <р2(у) с/у.  (17.40)

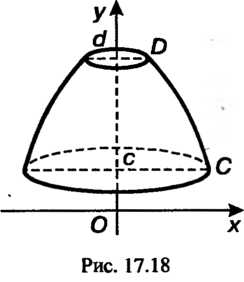
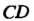
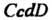
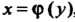
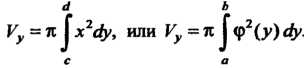
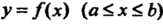Площадь поверхности, образованной вращением вокруг осиДуги кривой , определяется формулой

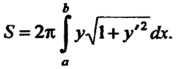(17.41)

Пример 17.22. Вычислить площадь поверхности, образованной вращением вокруг оси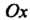Дуги линии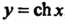, где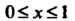(поверхность эта называется катеноидом).

Так как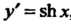, то по формуле (17.41) с учетом равенства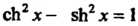

Получаем

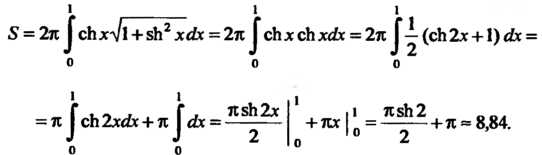
Пример 17.23. Вычислить объем тела, полученного вращением вокруг оси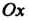Криволинейной трапеции, ограниченной параболой 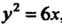прямой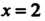И осью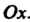

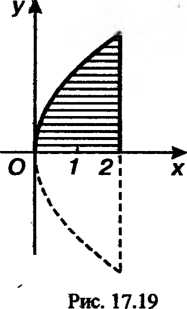
В соответствии с условием задачи находим пределы интегрирования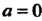, 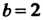(рис. 17.19).

По формуле (17.39) получаем

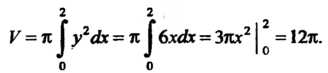
Пример 17.24. Найти объем тела, полученного вращением вокруг оси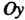 криволинейной трапеции, ограниченной параболой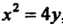, прямой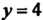И осью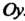

Замечая, что пределы интегрирования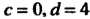, по формуле (17.40) находим

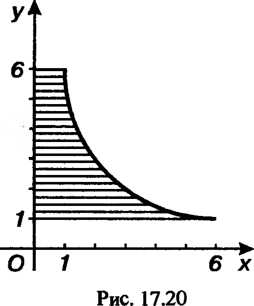
Пример 17.25. Найти объем тела, полученного вращением вокруг оси 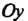Криволинейной трапеции, ограниченной гиперболой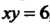, прямыми,

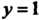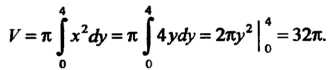
Из уравнения кривой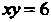Находим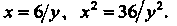

Принимая во внимание, что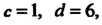По формуле (17.40) получаем

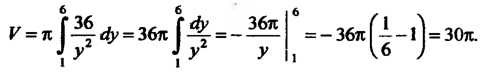
Пример 17.26. Вычислить объем тела, полученного вращением эллипса 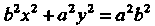Вокруг оси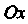(это тело ограничено эллипсоидом вращения). Из уравнения эллипса находим выражение для 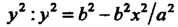По формуле (17.39) получаем

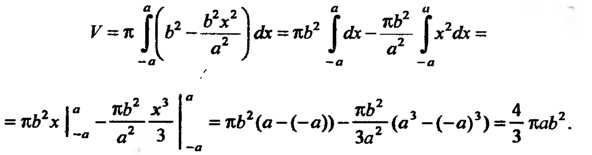
Следовательно,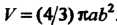. При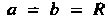Получаем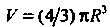

(объем шара).

Глава 18

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

< Предыдущая		Следующая >