17.8. Длина дуги кривой

Если линия задана параметрическими уравнениями

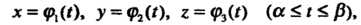
Где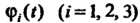- дифференцируемые функции аргумента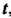, то дифферен

Циал длины ее дуги выражается формулой

(17.32)

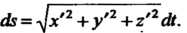
(17.33)

Интегрируя равенство (17.33) по промежутку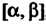, получаем формулу для вычисления длины дуги линии (17.32):

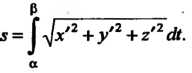
(17.34)

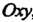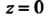Если линия (1732) лежит в плоскости,тоПри всех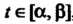, поэтому

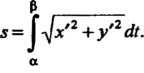
В случае, когда плоская линия задана уравнением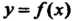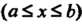, где

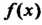- дифференцируемая функция, последняя формула принимает вид

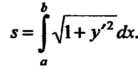(17.36)

Если плоская линия задана уравнением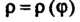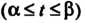В полярных

Координатах, то

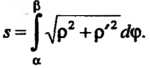(17.37)

Пример 17.18. Вычислить длину дуги линии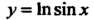Между точка

Ми, для которых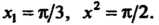

Искомую длину вычисляем по формуле (17.36).

Поскольку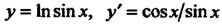, то

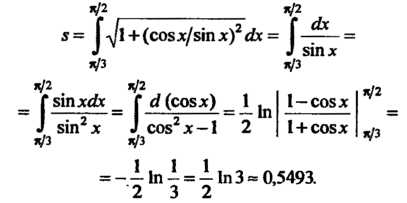
Пример 17.19. Найти длину дуги линии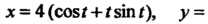

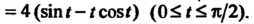
Применяем формулу (17.35), полагая в ней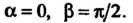 Так как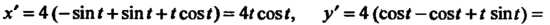

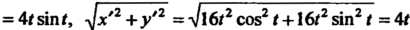, то

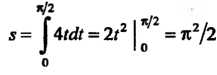
Пример 17.20. Вычислить длину дуги винтовой линии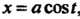 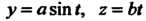Между точками, для которых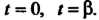

Поскольку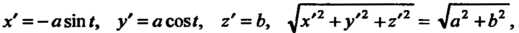То

По формуле (17.34) находим

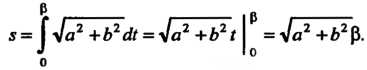
Пример 17.21. Найти длину кардиоды р = 2я(1-со5<р).

Так как р' = 2а5т<р, р2 +р'2 = 4я28т2ф+4а2(1-со5ф)2 = 8а2(1-

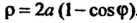
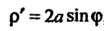
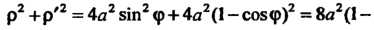
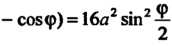
- со5ф) = 16а2 вт2 то по формуле (17.37) получаем

^ = 2^4а5т^¦«?ф = 16л^8^п-^¦«?Г^1 = -16асо5^¦ а  о

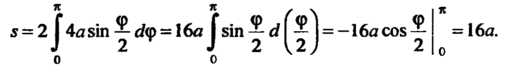
< Предыдущая		Следующая >