17.7. Площадь криволинейной фигуры

Площадь криволинейной трапеции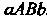, ограниченной сверху графиком функции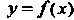, слева и справа - прямымиСоответственно,

Снизу - осью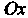(рис. 17.9), вычисляется по формуле

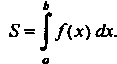(17.26)

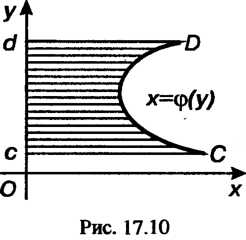
Площадь криволинейно трапеции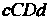(рис. 17.10), ограниченной справа

Графиком функции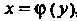, сверху и снизу - соответственно прямыми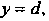

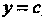, слева - осью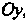, определяется формулой

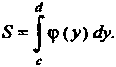(17.27)

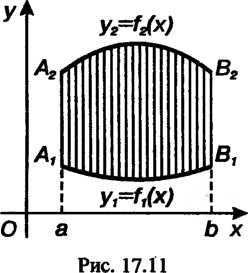
Площадь криволинейной фигуры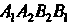, ограниченной сверху графиком

Функции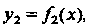, снизу - графиком функции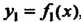, слева и справа -

Прямыми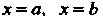(рис. 17.11), вычисляется по формуле

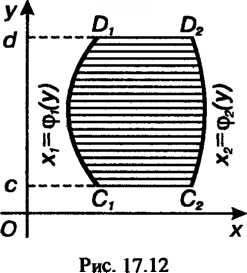
Площадь фигуры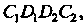Ограниченной слева и справа соответственно гра

Фиками функций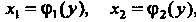, снизу и сверху - прямыми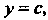

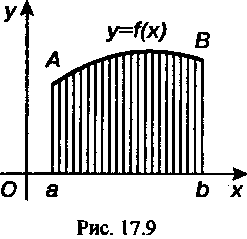
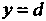(рис. 17.12), определяется формулой

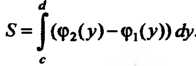(17.29)

Если линия, ограничивающая криволинейную трапецию сверху, задана параметрическими уравнениямиГде

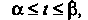
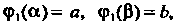То

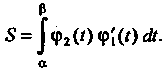(17.30)

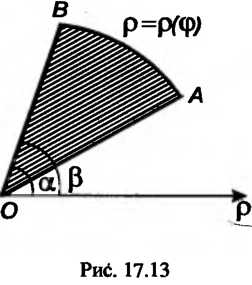
Площадь сектора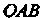(рис. 17.13), ограниченного дугой линии, заданной уравнением в полярных координатах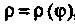, и двумя полярными радиусами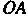

И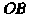, соответствующими значениям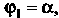 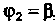, определяется формулой

Пример 17.13. Найти площадь фигуры, ограниченной линией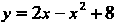И осью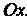

Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью 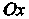(рис. 17.14). Решая систему уравнений

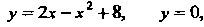
Получаем

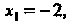
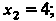Следовательно,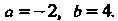

По формуле (17.26) находим

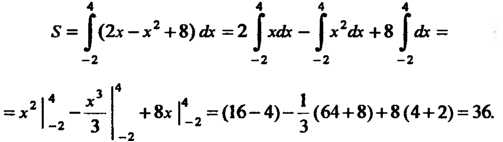
Пример 17.14. Найти площадь фигуры, ограниченной линией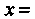 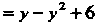И осью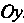

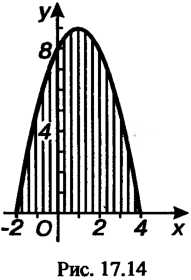
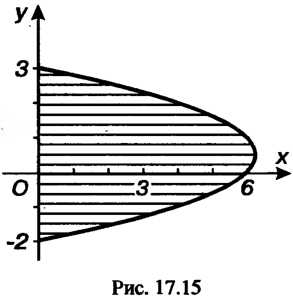
Данная фигура представляет собой криволинейную трапецию, прилежащую к оси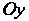(см. рис. 17.15). Найдем точки пересечения линии с осью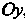, для чего решим систему уравнений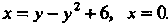. Из этой системы получаем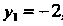

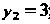; это означает, что в формуле (17.27), которой здесь необходимо пользоваться, нужно положить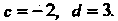

Следовательно,

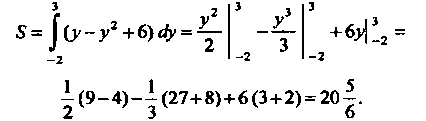
Пр имер 17.5, Вычислить площадь фигуры, ограниченной линиями

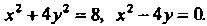
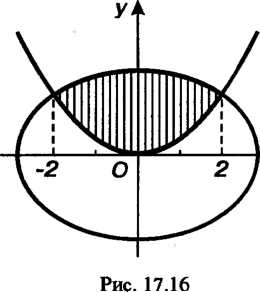
Данная фигура ограничена сверху дугой эллипса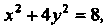Снизу - дугой пара

Болы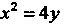(рис. 17.16).

Площадь вычислим по формуле (17.28).

Решая систему уравнений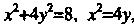 находим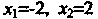- абсциссы точек пе

Ресечения заданных линий; следовательно,

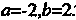’ Каждое из уравнений разрешаем

Относительно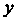

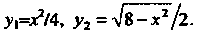
(В формуле (17.28) через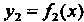 обозначена функция, график которой ограничивает фигуру сверху.)

Таким образом, искомая площадь

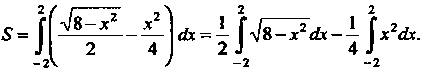
Для вычисления первого интеграла применим подстановку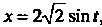, тогда

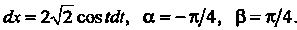
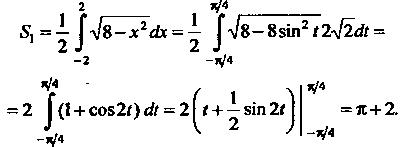
Поскольку

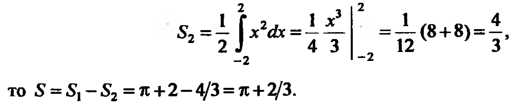
Пример 17.16. Вычислить площадь области, ограниченной эллипсом

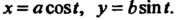
В силу симметрии эллипса относительно координатных осей достаточно вычислить площадь части области, лежащей в первой четверти, и результат умножить на 4. Заметим, что в этом случае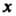Меняется от 0 до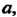Поэтому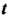Будет меняться от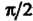До 0. По формуле (17.30) находим

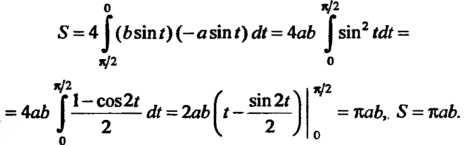
Замечание. В частном случае, когда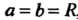, получаем-

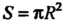Площадь круга радиуса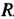

Пример 17.17. Вычислить площадь области, ограниченной лемнискатой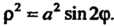

Принимая во внимание симметрию линии относительно ее оси (см. п. 2.10), по формуле (17.31) получаем

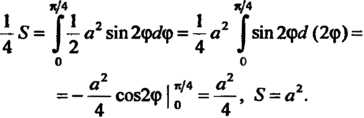
< Предыдущая		Следующая >