17.6. Интегралы Эйлера
Гамма-функция, или эйлеров интеграл второго рода, определяется формулой
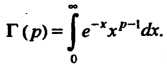 (17.19)
(17.19)
Этот интеграл является несобственным, так как верхний предел бесконечен; кроме того, при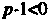 Подынтегральная функция не ограничена в окрестности точки
Подынтегральная функция не ограничена в окрестности точки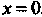 Интеграл (17.19) сходится при
Интеграл (17.19) сходится при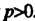 . Каждому положительному значению
. Каждому положительному значению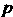 Соответствует вполне определенное значение
Соответствует вполне определенное значение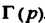 . Функция
. Функция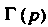 Не является элементарной. С Помощью метода интегрирования по частям можно доказать, что
Не является элементарной. С Помощью метода интегрирования по частям можно доказать, что
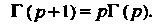 (17.20)
(17.20)
При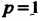 Интеграл находится непосредственно:
Интеграл находится непосредственно:
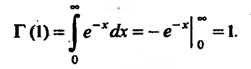
Подставляя в формулу (17.20) значения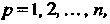 Получаем
Получаем
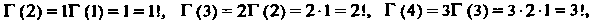
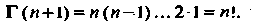 (17.21)
(17.21)
Итак, при натуральных значениях аргумента гамма-функция совпадает с факториалом, т. е. с функцией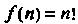 . Но гамма-функция определена не только при натуральных
. Но гамма-функция определена не только при натуральных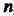 , но и при любых положительных значениях аргумента. Из формулы (17.21) следует, что можно считать
, но и при любых положительных значениях аргумента. Из формулы (17.21) следует, что можно считать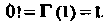 . График гамма-функции
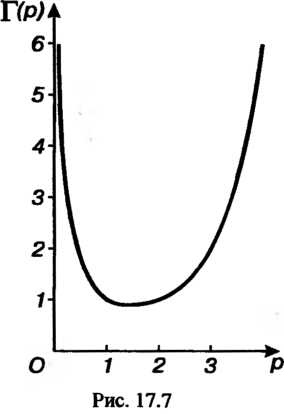
. График гамма-функции
Изображен на рис. 17.7.
Гамма-функция определяется и при отрицательных значениях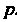 . В этот случае необходимо применить формулу (17.21), переписав её в виде
. В этот случае необходимо применить формулу (17.21), переписав её в виде
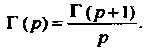 (17.22)
(17.22)
Если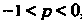 , то
, то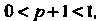 , поэтому правая часть формулы (17.22)
, поэтому правая часть формулы (17.22)
Имеет смысл, ею и определяется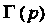 При этих значениях
При этих значениях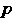 ; отметим, что в
; отметим, что в
Таком случае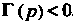 . Продолжая аналогичные рассуждения, убеждаемся в
. Продолжая аналогичные рассуждения, убеждаемся в
Т«щ«гго гамма-функция определена для всех отрицательных значений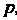 кроме
кроме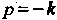 , где
, где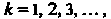 И кроме
И кроме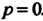
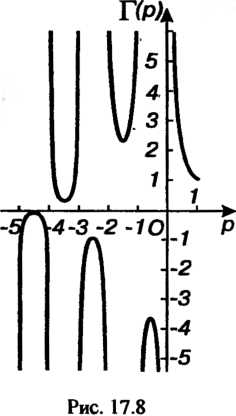
График гамма-функции при отрицательных значениях р изображен на рис. 17.8. Гамма-функция определена и для комплексных значений аргумента, кроме р ——к, к = 0Д2,...
Бета-функция, или эйлеров интеграл первого рода, определяется формулой
1
В(р,<?) = |^-1(1-хГ, Л. (17.23)
О
Подынтегральная функция не ограничена в окрестности точки х = 0 при р -1 < 0 ив окрестности точки х = 1 при <7 -1 < 0.
Интеграл (17.23) сходится при р> 0, <7 > 0.
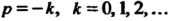
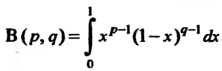
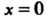
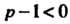
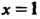
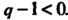
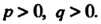
Значения бета-функции при различных значениях параметров р и? связаны между собой следующими соотношениями:
N.
В(р, д) = Ъ(д, р); В(р,<?) = ———В(р,<? — 1), ?>1;
Р+<7-1
Справедлива формула В (р, 1 - р) = я/зт рп, 0 < р < 1.
В случае комплексныхр яд интеграл (17.23) сходится, когдаКер> 0, Ке д> 0. Между бета - и гамма-функциями существует связь, выражаемая формулой
В(Р,?)=™7 (Р>0,*><)). (17.24)
Г (р+<7)
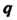
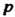
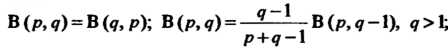
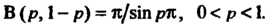
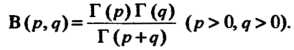
Пример 17.11. Вычислить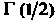 С помощью формулы(17.24).
С помощью формулы(17.24).
Полагая в формуле (17.24)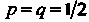 , получаем
, получаем
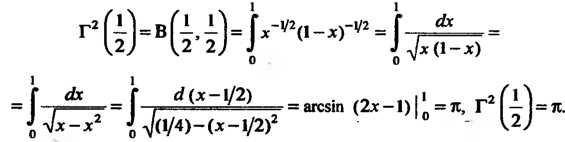
Так как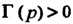 При
При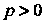 , то
, то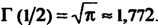
Пример 17.12. Вычислить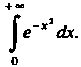
При вычислении этого интеграла используем результаты примера 17.11. Полагая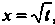 , находим
, находим
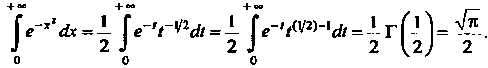
Следовательно,
(17.25)
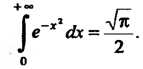
| < Предыдущая | Следующая > |
|---|