17.4. Оценка определенного интеграла. Теорема о среднем

Теорема 17.6. Если функция /(х) интегрируема на отрезке [о,6], где а<Ь, и для всех х € [а, 6] выполняется неравенство т< /(х)< М, то

Ь

(Ь-а)<^Г(х)Ах< М (Ь-а).  (17.10)

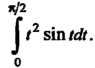
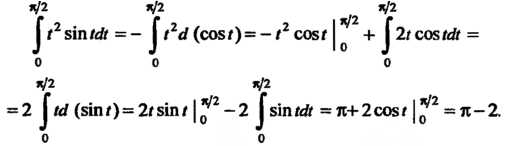
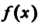
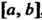
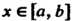
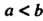
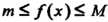
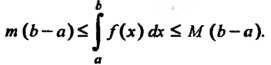
С помощью неравенств (17.10) можно оценить определенный интеграл, т. е. указать границы, между которыми заключено его значение. Неравенства (17.10) выражают оценку определенного интеграла.

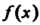
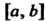
Теорема 17.7. Если функция /(х) интегрируема на отрезке [о,*] и для

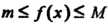
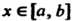
Всех х € [а, Ь]'выполняются неравенства т< /(х)< М, то

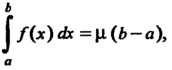
Ь

|/(*) Ах =ц (Ь-а),  (17.11)

А

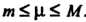
Где т<\1< М.

Эта теорема называется теоремой о среднем.

Замечание. В случае, когда функцияНепрерывна на отрезке

, равенство (17.11) принимает вид

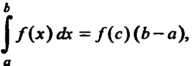(17.12)

Где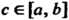

Число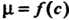, определяемое формулой

(17.12), называется средним значением функции 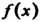На отрезке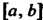

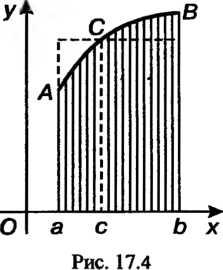
Равенство (17.12) имеет следующий геометрический смысл: площадь криволинейной трапеции, ограниченной непрерывной линией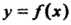

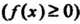, равна площади прямоугольника с тем же основанием и высотой, равной ординате некото

Рой точки этой линии (рис. 17.4).

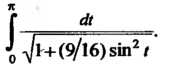
Пример 17.6. Оценить интеграл

Поскольку подынтегральная функция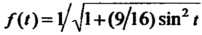В данном про

МежуткеИмеет наименьшее значениеИ наибольшее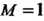, то в

Соответствии с формулой (17.10) получаем

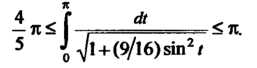
< Предыдущая		Следующая >