17.3. Замена переменной в определенном интеграле. Интегрирование по частям

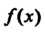
Теорема 17.4. Если выполнены условия: 1) функция /(х) непрерывна на отрезке [а, Ь\, 2) отрезок [а, Ь\ является множеством значений функции х = ф(/), определенной на отрезке а < / < р и имеющей на нем непрерывную производную: 3) ф (а) = а, ф (р) = Ь, то справедлива формула

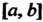
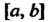
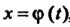
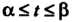
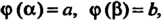
Теорема 17.5. Если функции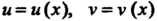Имеют непрерывные про

Изводные на отрезке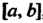, то справедлива формула

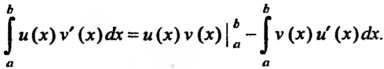(17.9)

Пр и м е р 17.3. Вычислить интеграл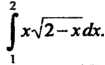 Введем новую переменную по формуле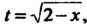Из которой получим

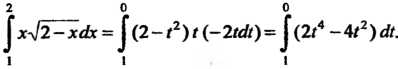
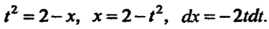
Вычислим новые пределы интегрирования с помощью формулы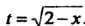. По

Скольку при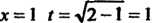, то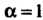; далее, при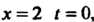Поэтому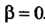

Формула (17.8) принимает вид

Вычисляя последний интеграл, находим

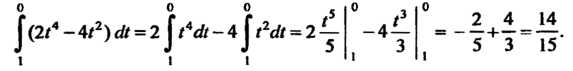
Следовательно,

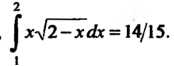
Пример 17.4. Вычислить интеграл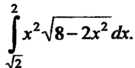

Введем новую переменную по формуле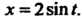Поскольку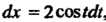

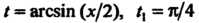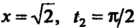ПриПри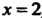, то

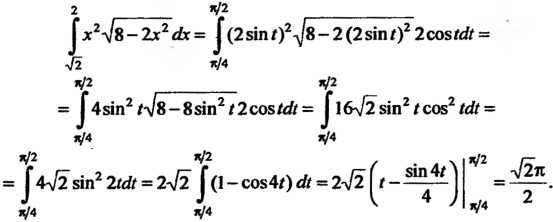
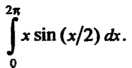
О

Интегрируя по частям, находим

2* 2* , 2я

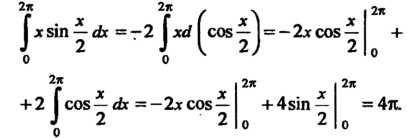
Ф

Пример 17.6. Вычислить интеграл ^ /25т/Л.

О

Дважды интегрируя по частям, получаем

Ф  ф  ф

1125тШ1 =- |/2</(сОБГ) = -/2СО8г|0 + ^2(СО5(А1 =

0  0  о

Ф ф = 2 (5Ш/)=2/5Ш/\^2-2 51ПШг =я+2собг |^2 =я-2. о  о

< Предыдущая		Следующая >