17.2. Определенный интеграл с переменным верхним пределом. Формула Ньютона - Лейбница
Рассмотрим функцию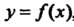
, интегрируемую на отрезке
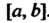. Если
,
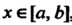То функция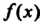
Интегрируема также на любом отрезке
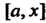. Предположим, что
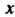меняется на отрезке
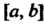, тогда на этом отрезке определена функция
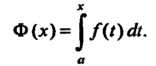
(17.6)
(Переменную интегрирования обозначили буквой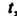
, переменный верхний предел - буквой
).
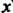Теорема 17.1. Если функция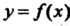
I интегрируема на отрезке
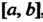, то
Функция (17.6) непрерывна на этом отрезке.
Теорема 17.2. Если подынтегральная функция непрерывна, то производная определенного интеграла с переменным верхним пределом существует и равна значению подынтегральной функции для этого предела, т. е.
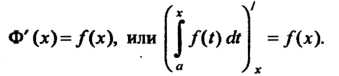
Следствие 1. Если функция
Непрерывна на отрезке
,топритобам
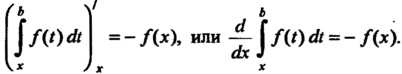
Следствие 2. Определенный интеграл с переменным верхним пределом является одной из первообразных для непрерывной подынтегральной функции.
Другими словами, для любой непрерывной функции существует первообразная.
Замечание. Интеграл с переменным верхним пределом интегрирования используется при определении многих функций. К таким функциям относятся, например:
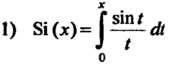(интегральный синус);
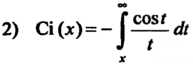(интегральный косинус);
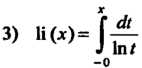(интегральный логарифм);
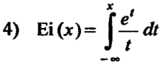(интегральная показательная функция);
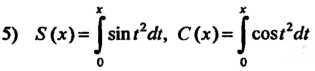(интегралы Френеля);
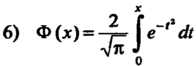(интеграл вероятностей).
Эти функции не являются элементарными; первообразные указанных подынтегральных функций не выражаются через элементарные функции.
Все приведенные функции хорошо изучены, для них составлены таблицы значений, эти функции находят широкое применение.
Связь между определенными и неопределенными интегралами выражает следующая теорема Ньютона - Лейбница, называемая основной теоремой интегрального исчисления.
Теорема 17.3. Определенный интеграл от непрерывной функции равен разности значений любой ее первообразной для верхнего и нижнего предела интегрирования:
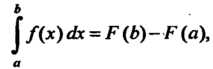(17.7)
Где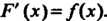
Формула (17.7) называется формулой Ньютона - Лейбница; ее можно переписать в виде
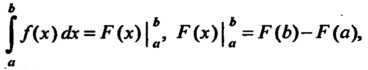
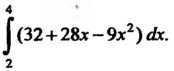
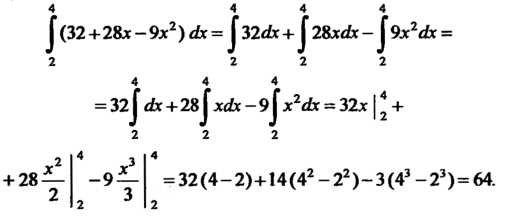
2
= 32(4—2)+14(4 —2 )—3(4 —2 ) = 64.
Ф
Пример 17.2. Вычислить интеграл ^ соз4 фЛр.
-Ф
Переменная интегрирования обозначена буквой ф. Преобразуя подынтегральную функцию, получаем
Сок4 ф = р-+С°5—^ ^ (1 + 2 С05 2ф + сок2 2ф).
Следовательно,
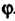
Ф Ф
^ С054 фС? ф = — ^ (I + 2 С052ф + С052 2ф) с/ф =
-ф - ф ф ф ф = — | сов2фе? (2ф)+— |(1 + соз4ф)с? ф =
-я/2 “V2 -я/2
1 I к/2 1 . _ I к}2 1 \к/2 1 . . | я/2 3
51П2ф —ф -51П4ф - — П.
4 ^ I -*}2 4 32 ^\-ф ^
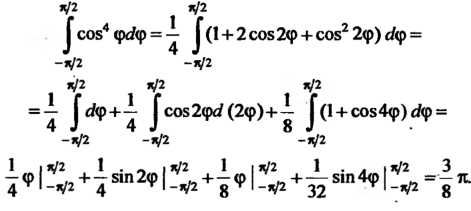
Левая часть второй формулы читается так: «двойная подстановка от в до Ь для функции Р(х)».
4
Пример 17.1. Вычислить интеграл ^ (32 + 28х-9х2)е1х.
2
Принимая во внимание свойства определенного интеграла, получаем
4 4 4 4
| (32 + 28*—9х2 ) ск = 132<&+128хс1х -19х2с! х =
2 2 2 2 4 4 4
= Зг|Л+2в|хс1х-9^хгйх = 32х \
| < Предыдущая | Следующая > |
|---|
