17.1. Определенный интеграл, Его геометрический смысл и свойства
Понятие определенного интеграла. Пусть дана функция у = /(х), определенная на отрезке [а, Ь\, где а <Ь. Отрезок [а, Ь\ точками а = х0 < < х, < х2 <. - - < х„_, <х„ = Ь разобьем на и элементарных отрезков [а, х,], [х,, х2, [х„_,, Ь\ длины которых обозначим через Ах*, т. е. Ах* =хк - х*_, (Л = 1,2,..., и, х0 = а, х„ = Ь). В каждом из элементарных отрезков [х*_1;х*] выберем произвольно одну точку!;*, значение функции в этой точке /(!;*) умножим на длину отрезка Дх*, получим произведение /(!;*) Дх*. Составим сумму всех таких произведений
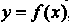
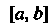
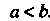
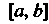
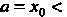
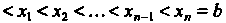
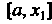
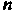
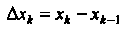
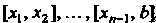
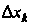
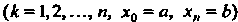
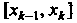
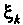
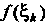
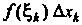
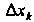
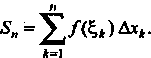
(17.1)
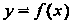
Сумма (17.1) называется интегральной суммой для функции у = /(х) на отрезке [а, Ь\
Обозначим через К длину наибольшего из элементарных отрезков [х*_,,х*] (Л = 1,2,..., и), т. е. X = шах Дх* (Л = 1,2,..., и).
Число 5 называется пределом интегральной суммы (17.1), если для любого числа е > 0 можно указать такое число 5 > 0, что при К < 5 выполняется неравенство 15„ - 51 < е независимо от выбора точек!;* на отрезках [х*_,,х*].
Определенным интегралом от функции у = /(х) на отрезке [а, Ь\ называется конечный предел ее интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю. Опре
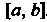
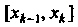
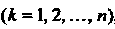
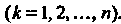
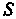
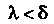
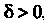
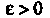
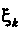
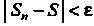
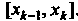
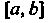
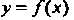
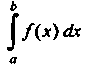
Интеграл от а до Ь); /(х) называется подынтегральной функцией, х - переменной интегрирования, а - нижним, Ъ - верхним пределами интегрирования. Следовательно, по определению
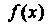
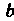
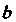
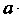
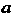
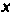
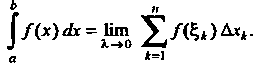
Из определения следует, что величина определенного интеграла не зависит от обозначения переменной интегрирования, т. е.
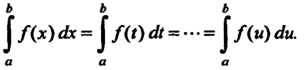(17.3)
Функция, для которой существует предел суммы (17.1), называется интегрируемой на отрезке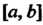
Очевидно, если функция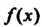
Интегрируема на отрезке
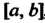, то она и ограничена на этом отрезке. Обратное утверждение не верно: существуют ограниченные функции, не являющиеся интегрируемыми. К ним относится функция Дирихле, равная единице в рациональных точках и нулю - в иррациональных. На любом отрезке [а, Ь\ эта функция ограничена, но не является интегрируемой на нем. Соответственно по определению
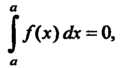(17.4)
Где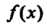
- любая функция;
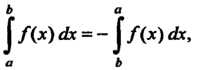(17.5)
Где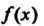
- функция, интегрируемая на отрезке
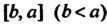Справедливы следующие утверждения.
1. Если, функция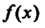
Интегрируема на отрезке
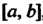, то она интегрируема на любом отрезке
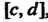, содержащемся в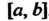
2. Если функция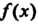
Непрерывна на отрезке
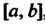, то она и интегрируема на этом отрезке.
3. Если функция f(x) имеет на отрезке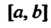
Конечное число точек разрыва первого рода, то она интегрируема на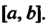
Геометрический смысл определенного интеграла. Если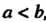
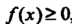, то
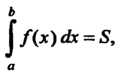
Т. е. определенный интеграл от функции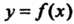
По отрезку
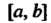Равен площади
Криволинейной трапеции, ограниченной сверху графиком функции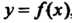
, слева
Неправа - отрезками прямых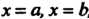
, снизу - отрезком оси
(рис. 17.1).
Если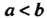
И
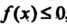,то
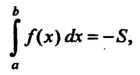
Т. е. определенный интеграл от функции, принимающей неположительные значения, равен площади соответствующей криволинейной трапеции, взятой со знаком минус (рис. 17.2).
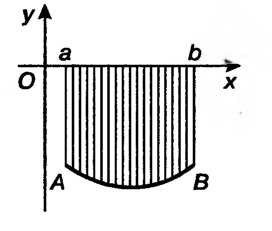
Рис. 17.2
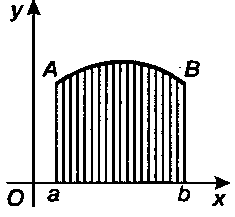
Рис. 17.1
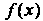
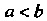
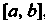
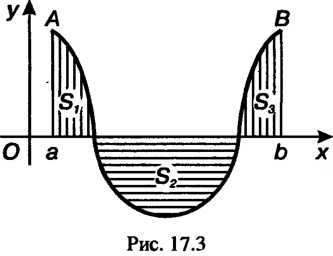
Если а < Ь и Дх) меняют знак на отрезке [а, Ь], то определенный интеграл равен
Алгебраической сумме площадей соответствующих криволинейных трапеций (рис. 17.3):
Ь
Г /(х)дх = 5] —52 +^3.
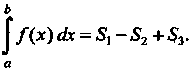
Основные свойства определенного интеграла. Определенный интеграл обладает следующими свойствами.
1. Если функция /(х) интегрируема на наибольшем из отрезков [а, Ь\, [а, с], [с, Ь\, то она интегрируема на двух отрезках, причем
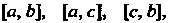
V С. V
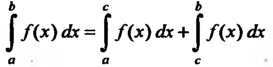
| /(*) | Дх) дх+| Дх) дх
А а с
При любом расположении точек а, Ъ,с.
2. Если функция / (х) интегрируема на отрезке [а, Ь], то функция
К /(х), где к = сош1, также интегрируема на этом отрезке, причем
^ к Дх) дх = к ^/(х) дх.
3. Если функции Дх) и ф(х) интегрируемы на отрезке [а, Ь\, то их сумма и
Разность также интегрируемы на этом отрезке, причем ь ь ь
| (Д*)± Ф (*)) | Дх) дх ± | ф (х) дх.
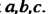
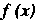
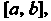
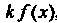
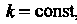
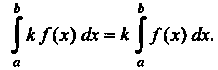
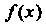
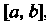
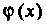
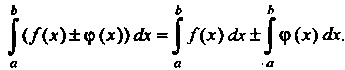
4. Если функция/х) интегрируема на отрезке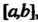
,где
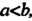И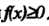
Цлявсех
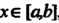,то
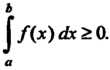
5. Если функции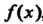
,
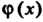Интегрируемы на отрезке
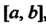, где
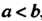, и
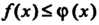Для всех
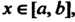То
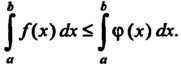
6. Если функция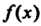
Интегрируема на отрезке
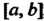, где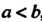
, то функция
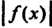Также интегрируема на
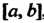, причем
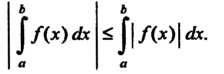
| < Предыдущая | Следующая > |
|---|
