16.8. Интегрирование некоторых тригонометрических выражений

Неопределенные интегралы вида

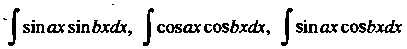(16.28)

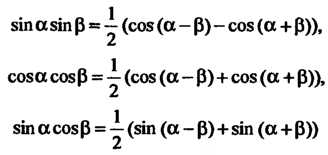
Приводятся к интегралам

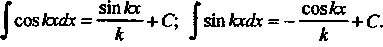
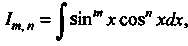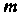Неопределенные интегралы ввдаГдеИ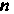—натуральные

Числа, находятся с помощью тригонометрических формул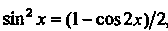

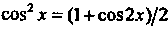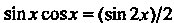,, есл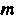иИ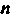Четные.

Если хотя бы одно из чисел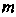И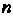- нечетное, то от нечетной степени отделяется множитель и вводится новая переменная. В частности, если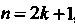, то

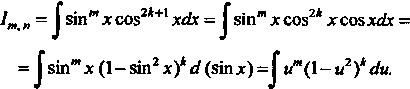
Последний интеграл находится непосредственно (как интеграл от алгебраического многочлена).

Неопределенный интеграл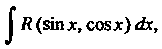Где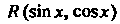- рацио

Нальная функция от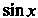И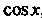, путем введения новой переменной по формуле

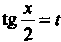
(16.29)

Приводится к интегралу

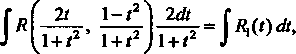
Где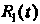- рациональная функция переменной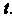. Пример 16.31. Найти интеграл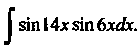

Это первый из интегралов типа (16.28), в данном случае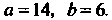

Применяя первую из приведенных выше тригонометрических формул, преоб-

Разуем подынтегральную функцию и интегрируем:

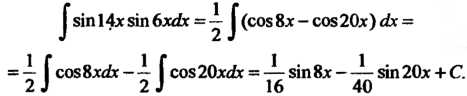
Пример 16.32. Найти интеграл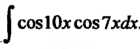 Преобразуя подынтегральное выражение, находим

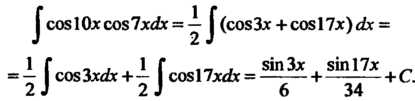
Пример 16.33. Найти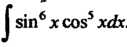

Поскольку одна из степеней является нечетной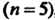, то интеграл можно

Найти следующим образом:

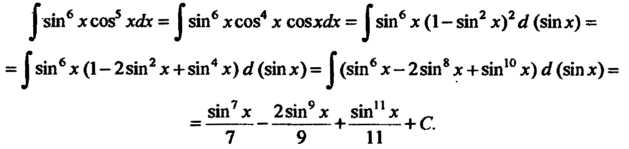
Пример 16.34. Найти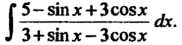 Преобразуя подынтегральное выражение, получаем

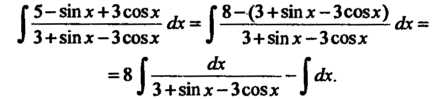
Чтобы найти первый интеграл, применим подстановку (16.29):

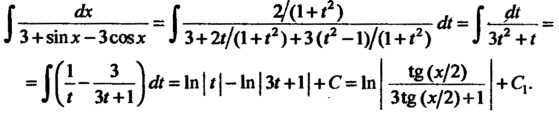
Следовательно,

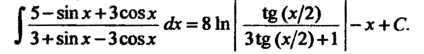
Глава 17

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

< Предыдущая		Следующая >