16.7. Интегрирование простейших иррациональных функций
Неопределенный интеграл Г, *** выделением полного квадрата в
У4ах2+Вх + С
Подкоренном выражении и введением новой переменной и = х+Ь в зависимости от знака Л приводится к одному из интегралов:
Г *........= агсзт—+ С, (16.19)
^ л/а2 - и2 а
Неопределенный интеграл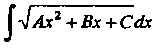
В зависимости от знака
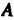Приво
Дится к одному из интегралов:
(16.21)
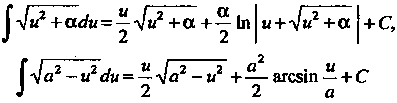(16.22)
(см. формулы (16.13) и (16.14)).
Неопределенный интеграл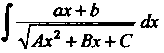
Приводится к интегралам вила
(16.23)
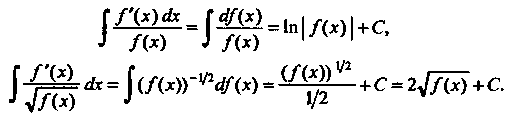(16.24)
Интеграл вида
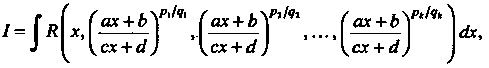(16.25)
Где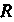
—рациональная функция и
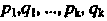— целые числа, с помощью подстановки
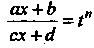(16.26)
Где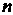
- наименьшее общее кратное чисел
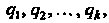Приводится к
Интегралу от рациональной функции.
Интеграл от дифференциального бинома
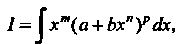(16.27)
Где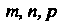
- рациональные числа;
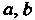- постоянные, отличные от нуля, сво
Дится к интегралу от рациональной функции в трех случаях:
1) когда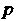
— целое число, — разложением на слагаемые по формуле бинома Ньютона при
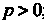; подстановкой
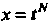, где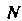
- общий знаменатель дробей
;
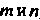2) когда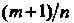
- целое число, — подстановкой
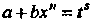, где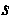
-знаменатель дроби
;
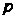3) когда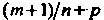
- целое число, - подстановкой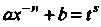
' л/Зх2 +6х+4 ^^Г+1?+^3 = ^1п|(х+1)+^0с + 1)"+^ Пример 16.26. Найти ^л/х^+бх+13лбе.
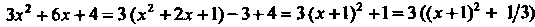
Так как Зх2+6х+4 = 3(х2+2х+1)-3+4=3(х+1)2+1 = 3((х+1)2 + 1/3), то, положив х+1 = и, по формуле (16.20) получим
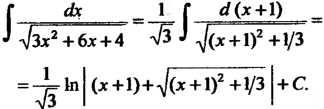
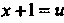
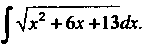
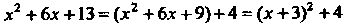
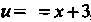
Поскольку х2 +6х + 13 = (х2 +6х+9)+4 = (х+3)2 +4, то, полагая и= =х+3, по формуле (16.21) находим
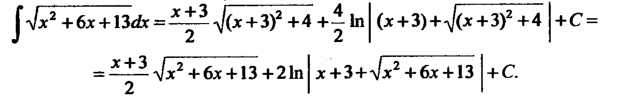
= ^±^л/х2+6х + 13+21п х+3+л/х2+6х + 13 2
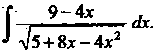
Пример 16.27. Найти Г 9 -------лбе.
М5 + 8х-4х2
Поскольку (5+8х - 4х2 )' = 8 - 8х = - 8 (х -1), 9 - 4х = -4х +4+5= -4 (х -1)+5, 5+8х—4х2 =—4((х2-2х + 1)-1)+5 = -4(х-1)2 +9=4х х(9/4-(х-1)2), тона основании формул (16.19) и (16.24) получаем
Г, 9~4*........А-Г -4^-1>+5 <ь= Г +
3 -\/5+8х-4х2 -» -\/5+8х-4х2 ¦' л/5+8х-4х2 + Г 5йЬс -1 Г —8(х-1)<& |Г Г </(*-!) _
' л/5 + 8х-4х2 2-» л/5+8х-4х2 ' 2^9/4-(
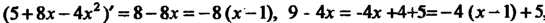
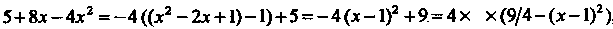
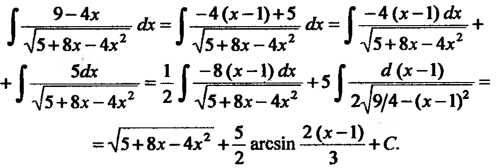
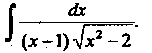
Пример 16.28. Найти интеграл |-
СЬс
* (х-1)^х2 -2*
/ Перейдем к новой переменной Г по формуле х-1 = 1/1, откуда <1х = = - й/12, х2-2 = (1+21-12)/(2.
Следовательно,
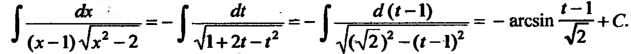
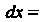
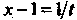
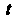
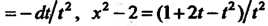
Г _ Г _агС8ш 1=2
¦» (х-1)л/х2 —2 ^ л/1 + 2Г-Г2 -^(л/2) -(Г-1)2 ^2
Возвращаясь к переменной х, находим
Г • л/2(х-2)
I-, = агсзт--—г^ + С.
* (х —1)л/х2-2 2(х-1)
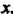
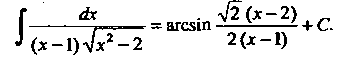
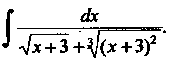
Это интеграл вида (16.25), причем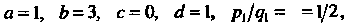
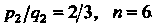. Подстановка (16.26) принимает ввд
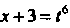. Отсюда следу
Ет, что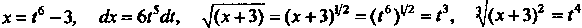
,
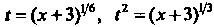. Таким образом,
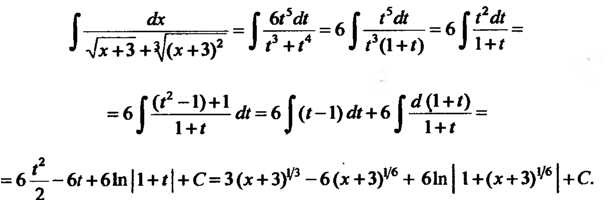
Пр имер 16.30. Найти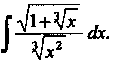
Переписав интеграл в виде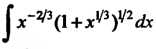
И сравнив с интегралом (16.27),
Заключаем, что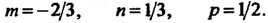
Так как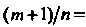
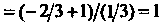Есть целое число, то имеем второй случай интегрируемости дифференциального бинома. Подстановка
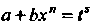В данном случае примет
ВВД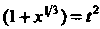
, откуда
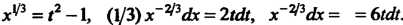Под-
Старив эти выражения в интеграл, получим
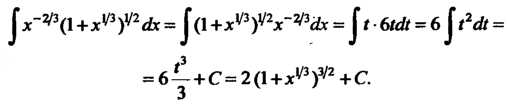
| < Предыдущая | Следующая > |
|---|
