16.6. Интегрирование рациональных функций
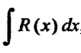
Рассмотрим неопределенные интегралы вида ^ /? (х) Ах, где К (х) -
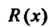
Правильная рациональная дробь, т. е.
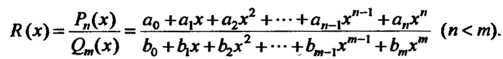
Д _ РЛ*) _ а0+а1х + а2х Н Нои_[Х + аГ1х ^ »
&(*) Ь0+Ь1х+Ь2х2 + ¦¦¦+ Ът_,хт~' + Ьтхп
Нахождение указанных интегралов основано на разложении рациональной
Дроби в сумму элементарных дробей, т. е. дробей вида
А Вх + С
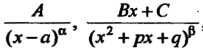
(х-я)“’ (х2 + рх+дУ5’ где а, р - натуральные числа; а, р, д, А, В, С - действительные числа; р2/4-<? < 0 (корни трехчлена являются комплексными).
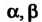
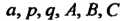
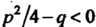
Это разложение определяется теоремой 8.5 (см. п. 8.7).
Так как -- - г—— = ——+~т~—~ (см. пример 8.18), то х +1 х+1 х2-х+1
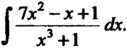
Пример 16.22. Найти Г7- с1х.
^ х3+1
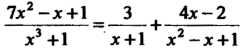
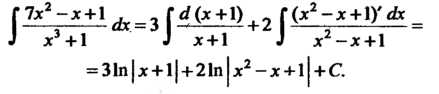
Г7х2-х + 1 ГА(х+1) „ Г(х2-х + Х)'Ах _
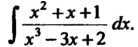
Поскольку
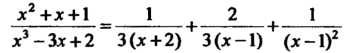
Х - Зх + 2 3(х+2) 3(х-1) (х-1)
(см. пример 8.19), то
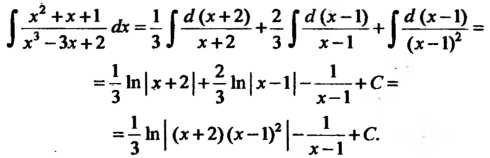
Г х2 +х+1 ±с_ \ Г с? (х + 2) ( 2 Г</(х-1) , М(х-1)_ ^ х3 - Зх + 2 3^ х+2 3^ х —1 ^ (х-1)2
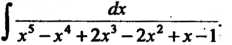
Пример 16.24. Найти интеграл I - г-—
^ х —з
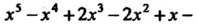
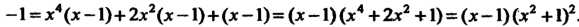
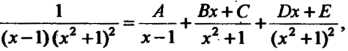
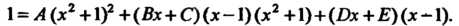
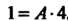
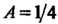
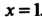
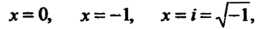
Х —х +2х —2х +х-1 Разлагая знаменатель на множители, получаем х5-х4+2х3-2х2+х--1 = х4(х-1)+2х2(х-1)+(х-1)=(х-1)(х4+2х2 + 1) = (х-1)(х2 +1)2.В данном случае разложение в сумму элементарных дробей должно иметь вид
_1__ А Вх + С Бх+Е
(х —1)(х2 +1)2 х-1 х2 +1 (х2 +1)2 ’
Откуда
1 = А (х2 + 1)2 +(Дх + С)(х —1)(х2 + 1)+(/)х + .Е)(х —1).
Полагая в этом тождестве х = 1, находим 1 = А -4, т. е. А = 1/4. Придавая х соответственно значения х = 0, х = — 1, х = * = ^/—1, получаем уравнения
1 = А-С-Е; 1 = 4А+4В-4С+2В-2Е; 1 = (Ш+Е)0-1), или 1 = = —0—ГН+Е1-Е, т. е. 1 = - И - Е + ( Е - П) I, откуда 1 = - Б-Е, Е-Б = 0. Решив полученные уравнения, найдем В = —1/4, С = —1/4,0= —1/2, Е=—1/2. Таким образом,
Г_Ах__г( 1 х + 1 х + 1
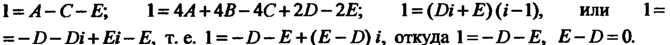
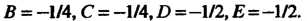
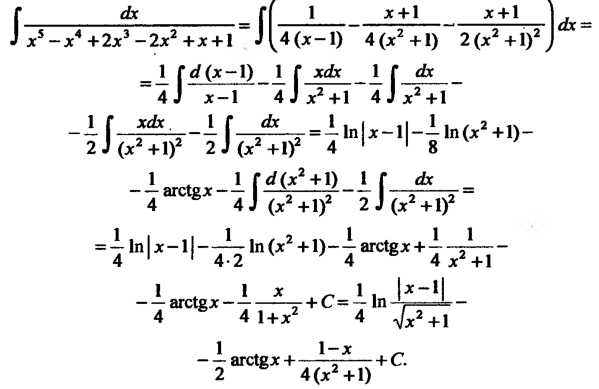
Замечание. Интеграл Г—,*** , найден с помощью подстановки
3 (х +1)
^ х5 - хА +2х3 - 2х2 +х + 1 (^4(х-1) ~ 4 (х2 + 1) ~ 2 (х2 +1)2 }
= 1 Г^С*-1) 1 Г хАх 1 Г Ах 4 ^ х-1 4 ^ х2 +1 4 ^ х2 +1
-I Г—5-ЁЦ—1 Г * =11п|х-1|-11п(х2-И)-
2 ^ (х2 +1) 2 ^ (х2 +1) 4 1 1 8
-АапЛ*-! Г^±*>-1 Г.........Ф__ =
4 8 4.!(х2+1)2 2 ^ (х2 +1)2 = — 1п I х—11—^1п(х2+1)--|-агс18х+-7 1
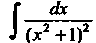
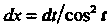
Х = 1®,‘ Так как Ах = А1/соз21, то
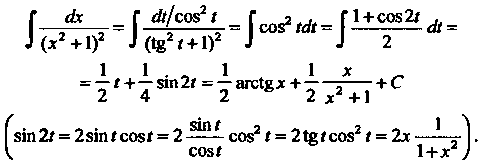
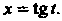
Г.......Р--т= Г-^^= Гсо82гл= Г1+с082'<&=
^ (х +1) .!(1е2г+1)2 ^ Л 2
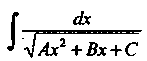
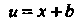
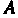
| 8т2? = 281ПГС08Г = 2 С082 I = 21е<С082 I = 2х —^-=-1.
СозГ 1+х у
| < Предыдущая | Следующая > |
|---|